Комплексное усиление пропускной и провозной способности железных дорог. Основные принципы организации и управления пассажирскими перевозками. Пригородные пассажирские перевозки, страница 58

Существенное влияние на возможность решения задачи оказывает ее размерность, которая зависит от числа переменных и числа ограничений. Для расчетной сети железных дорог СНГ число элементов множества 1₂·n = 400, при этом число возможных назначений поездов составит 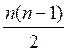. Число дуг (ij) расчетной сети к = 835. Поэтому количество переменных составит n(n-1)к/2= 7∙10⁷.

Число корреспонденции пассажиропотока определяется исходными данными о пассажиропотоках. Для сети в целом информация о пассажиропотоках агрегирована и представлена в виде матрицы межрайонных корреспонденции, включающей 250 опорных районов (число элементов множества I₁). Поэтому максимальное число струй пассажиропотока составит 3∙10⁴, а число переменных составит 21∙10¹¹.

Число маршрутов поездов определенного назначения может быть астрономическим, однако для практических целей оно ограничено десятью маршрутами. Поэтому суммарное число маршрутов всех назначений составит 8∙10⁵ . Объем исходной информации также достаточно велик. Число ограничений по освоению пассажиропотока равно числу дуг расчетной сети (835), а по обеспечению заданного уровня беспересадочного сообщения порядка 10 тыс. Число ограничений по пропускной способности составляет 835, а по перерабатывающей способности станций-400.

В таких условиях приведенная модель задачи даже для фиксированного момента времени имеет громадную размерность, и решение задачи невозможно даже с применением современных и перспективных ЭВМ. Это вызывает необходимость упрощения модели для сети железных дорог и исследование взаимосвязи отдельных параметров и влияния их на функционирование системы в целом. Для возможности решения на сетевом уровне необходимо ввести в модель следующие упрощения и допущения:

число назначений и маршрутов следования поездов выбирается для заданного периода времени. Обычно расчетный период соответствует месяцу, так как именно за этот период задается информация о пассажиропотоках;

при расчете числа и назначений пассажирских поездов, которые обеспечивают освоение пассажиропотока, можно не учитывать распределение пассажиропотока по поездам, а использовать обобщающий параметр - густоту пассажиропотока на участке.

Значения густоты можно с достаточной степенью точности моделировать, не определяя переменных , а используя только величины струй пассажиропотоков. В этом случае функционал Е не зависит от переменных , при этом  можно принять равным нулю. Учитывая необходимость ограничений по вагонному парку и приведенные упрощения, задачу расчета плана формирования пассажирских поездов можно сформулировать в следующем виде:

пусть I_pq – число поездов назначения pq, тогда:

, где p – индекс станции формирования; q – индекс станции оборота;  – число вагонов к-й категории в поезде назначения pq;  – число составов в обороте для назначения pq.

Ограничение по освоению густоты пассажиропотока на участках

,                                                (38.1)

где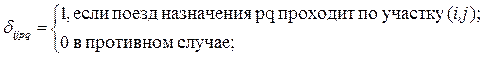  

а_к – вместимость вагона к-й категории; Г_ij – густота пассажиропотока на участке (i,j).

Ограничения по перерабатывающей способности станции формирования

.

Ограничения по перерабатывающей способности станции оборота

Ограничения по величине вагонного парка дороги S

, где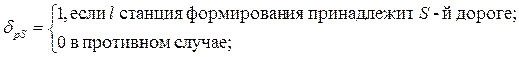

Ограничения по обеспечению уровня беспересадочных сообщений. Если, то

, где  – номер станции зарождения пассажиропотока;  – номер станции погашения пассажиропотока;  – величина корреспонденции пассажиропотока из в; R – заданный уровень беспересадочных сообщений;

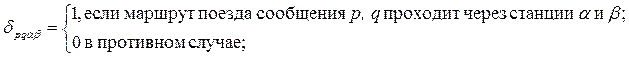
Ограничения по пропускной способности участков

.

При наличии параллельных ходов ограничения (38.1) несколько изменяются и составляются по сечениям. В правую часть неравенств записывается густота перспективного пассажиропотока по всем участкам рассматриваемого сечения.