Комплексное усиление пропускной и провозной способности железных дорог. Основные принципы организации и управления пассажирскими перевозками. Пригородные пассажирские перевозки, страница 66

Так как определитель отличен от нуля, система совместна и имеет одно решение, корни выражены формулами Крамера:

;   ;   .

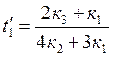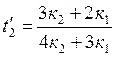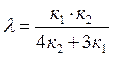Полученные значения неизвестных выражаются только через к₁, к₂, т.е. являются функцией темпа накопления струй пассажиропотоков. Для условий рассматриваемого примера:

;

.

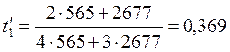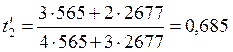Рассматриваемый пример рассчитан в условиях, когда зависимость пассажиропотока от времени линейна для всех назначений струй. Если такая зависимость соответствует каждой струе пассажиропотока, определить время отправления можно тем же методом с некоторым изменением условий.

39.5. График оборота пригородных поездов

Задача построения графика оборота пригородных составов состоит в увязке «ниток» графика движения в единый график оборота, представляющий замкнутый контур маршрутов с минимальным числом потребных составов с учетом периодичности проведения осмотров и ремонтов моторвагонного подвижного состава в соответствии с планово-предупредительной системой ремонта, принятой на железных дорогах. График оборота должен обеспечивать равный межремонтный пробег составов в маршрутах.

Для того чтобы в дальнейшем не выделять деповскую станцию из числа п станций оборота, введем фиктивную станцию оборота, моделирующую депо, на которую ежесуточно должно заходить для ремонта М_р составов и соответственно М_р пар фиктивных «ниток» графика. Каждая «нитка» при построении графика оборота однозначно определяется расписаниями отправления Т и прибытия iпо начальной и конечной станциям оборота.

В любой момент времени т число составов М, обслуживающих пригородный участок, складывается из числа составов, находящихся в движении и на промежуточных остановочных пунктах каждой зоны М_х, и числа составов М_n, простаивающих в этот момент на станциях оборота: М = М_х + М_n.

Так как составы не покидают участок, то М зависит не от выбранного момента времени т, а только от способа увязки «ниток» графика в оборот. Удобно рассмотреть момент разреза графика t_раз, считая, что в этот момент времени все составы простаивают на станциях оборота (обычно разрез графика осуществляют ночью). Тогда

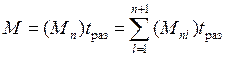, где  – число составов, простаивающих в момент разреза графика на станции l.

Так как значения независимы, то

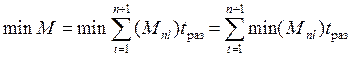
Поэтому задача о минимизации общего числа составов, обращающихся на участке, распадается на (п + 1) задачу минимизации числа составов, простаивающих в момент разреза графика на каждой станции оборота.

На станции l заданы расписания прибытия  и отправления  поездов, где;  (N_l – число ниток графика). Пусть  – технологически необходимая норма времени оборота составов на станции l. Обозначим = к. Расписания прибытия с учетом времени оборота  и расписания отправления поездов делят временную ось, соответствующую станции оборота, на отрезков. Для простоты изложения можно считать, что .Поставим в соответствие каждому из этих отрезков число к_V – равное числу составов, находящихся в этот промежуток времени на станции оборота. Очевидно, что после каждого прибытия поезда число составов увеличивается, а после каждого отправления - уменьшается на единицу min; .

В противном случае хотя бы один состав будет простаивать в течение целых суток на станции обо рота. Это дает возможность определить все к_v, в том числе и к₁ = к.

Для рис. 39.6 ; отсюда к = 1.

Рисунок 39.6 – Фрагмент графика для определения числа составов, простаивающих на станции оборота

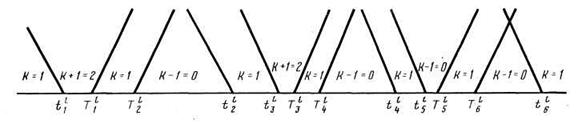
Расписание прибытия может быть увязано с расписанием отправления без увеличения числа составов только в том случае, если индексы  для всех отрезков, принадлежащих . В противном случае увязка соответствующих расписаний приведет к увеличению общего числа составов. Для рассматриваемого примера расписание может быть увязано либо с ,либо с. Увязать с  нельзя, так как такая увязка приведет к увеличению потребного числа составов на единицу.

Для формализации описания алгоритма построения графика оборота по каждой станции оборота целесообразно ввести матрицу возможных увязок ниток:

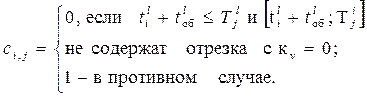
Для рассматриваемого примера при  представлена матрица 39.1 возможных увязок.