![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
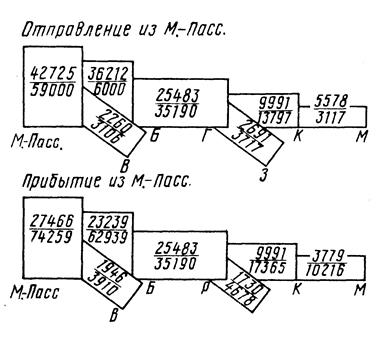
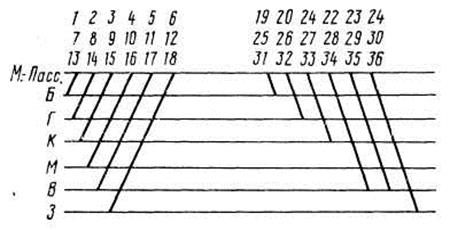
Условия равенства «ниток» прибытия и отправления для составов одной категории по каждой станции возможного оборота могут быть представлены:
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Целевая функция имеет вид:
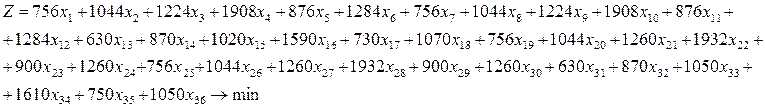
На прямолинейном направлении, включающем п станций формирования и оборота пригородных поездов, задана схема их прокладки за некоторый период. Требуется определить интервалы следования между поездами, при которых достигается минимальное количество пассажиро-часов ожидания по начальной станции (как возможный вариант в целом по направлению). Зависимость пассажиропотока от времени принять линейной.
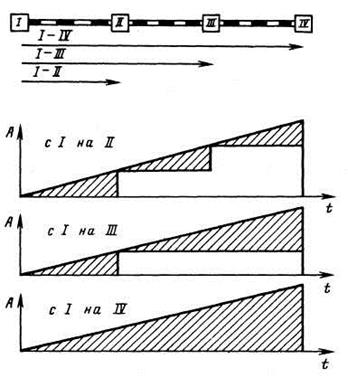
В системе координат t, А (время, пассажиропоток) пассажиро-часы ожидания численно равны площади, ограниченной кривой нарастающего итога пассажиропотока и ступенчатой линией, характеризующей принятое расписание (рис. 39.5). Если вводить кривую нарастающего итога пассажиропотока асимптотически в виде приближенной зависимости от времени, то площадь Ф, ограниченная ступенчатой линией и осью абсцисс, будет функцией искомых значений времени отправления, зависящей от вида аппроксимирующей кривой.
Минимум пассажиро-часов ожидания или максимум площади Ф можно определить, приравняв к нулю частные производные этой функции по ti, причем i (число независимых переменных) на единицу меньше заданного числа проездных единиц. Значения интервалов между поездами будут найдены решением полученной таким образом системы уравнений. При линейной зависимости пассажиропотока от времени получается система линейных алгебраических уравнений, решение которой определяет такие значения точек отправления, при которых достигается минимум площади, ограниченной прямой и ступенчатыми линиями, выражающими потребность в отправлении и предлагаемое отправление.
Если линия нарастающего итога пассажиропотока может быть выражена линейной зависимостью от времени, то площадь ступенчатой фигуры при отправлении трех поездов (см. рис. 39.5) составит:
![]() , где
, где ![]() ,
,![]() – соответственно интервалы между отправлением первого и второго
поездов в долях рассматриваемого примера; к – коэффициент пропорциональности в линейной зависимости пассажиропотока от времени.
– соответственно интервалы между отправлением первого и второго
поездов в долях рассматриваемого примера; к – коэффициент пропорциональности в линейной зависимости пассажиропотока от времени.
Тогда неизвестные ![]() и
и ![]() определятся из
выражений:
определятся из
выражений:
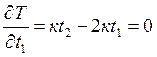 ;
;
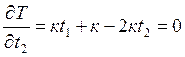 ;
;
откуда t1 = 1/3; t2 = 2/3, т. е. в случае линейной зависимости пассажиропотока от времени целесообразно равномерное распределение поездных единиц в рассматриваемом периоде независимо от темпа накопления струи пассажиропотока. Если число зонных станций больше двух, то между переменными есть дополнительные связи, выражающиеся в том, что для данного варианта плана формирования могут быть приняты дополнительные условия, число которых равно числу транзитных поездов. Тогда минимум пассажиро-часов можно определить методом неопределенных множителей Лагранжа.
|
для станцииI A1 = k1t; |
|
для станции II А2 = k2t; |
|
для станции III A3 = k3t. |
Пример. На направлении с четырьмя станциями пассажиропотоки линейно зависят от времени. Для заданной схемы прокладки требуется найти периоды отправления, при которых достигается минимум пассажиро-часов ожидания. Зависимости, характеризующие изменение пассажиропотока от времени.
Абсолютная величина времени суток значения не имеет, так как пассажиро-часы рассчитываются в интервалах между отправлением поездных единиц. Тогда уравнения примут вид:
по станции I
![]() ;
;
по станции II
![]() ;
;
по станции III
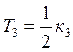 .
.
Дополнительное условие ![]() .
.
Функция Лагранжа имеет вид
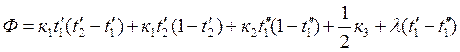 .
.
Далее получаем систему уравнений:
![]()
![]() ;
;
![]()
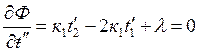 ;
;
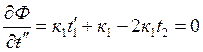 ;
;
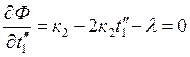 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.