Формы проявления значений нормативных показателей в разных сферах, страница 48

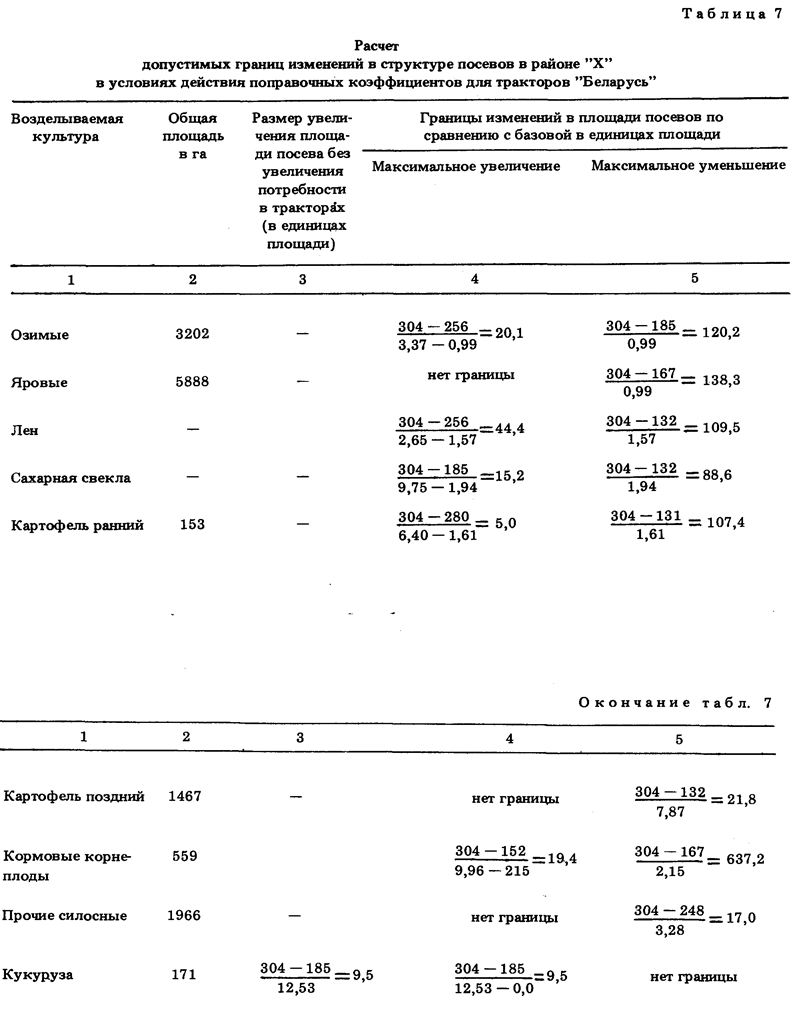
Во-вторых, поправочные коэффициенты могут найти широкое применение и при определении оптимальной (с точки зрения экономии ресурсов) структуры посевных площадей.

3.2. ОБ ОДНОМ ПОДХОДЕ К ГРУППИРОВКЕ НОРМИРУЕМЫХ ОБЪЕКТОВ

В § 1.4 говорилось о методе расчета нормативов на основе объектов-представителей. Но чтобы выбрать объект-представитель, нередко приходится все множество объектов сводить в группы по каким-то заданным признакам. Известны три вида соединения элементов: размещения (А"^ = n(n-1)(n-2)...(n-m+

+П- гтрг>рртяипт1т<-и (Р = 1-2>3---п = п!> и р.пепинения

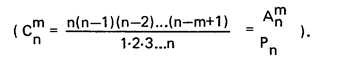
Однако упомянутые виды соединения элементов (а, Ь, с, ...z) не охватывают того случая, когда в соединении постоянно присутствуют все элементы (п = т), но сами элементы по определенным признакам делятся на какое-то целое число X, которое одинаково или отлично для каждого элемента Хд a£ Х^ ... а=Х^ либо XgSiX^... =йХ^,гдеХ=2,3...оо.

Проиллюстрируем это на примере. В хозяйстве N имеется Р полей, которые отличаются друг от друга по каменистости (элемент а ), рельефу (Ь), механическому составу почв (с) и длине гона (d). Но такая характеристика полей фактически ничего не выражает, потому что количественно не характеризует ни рельеф, ни почвы, ни каменистость полей. Требуется ввести новые характеристики отдельных элементов, для чего проведем дробление (деление) элементов по определенным признакам. Рельеф может быть ровным и с уклоном (2 вида), каменистость может быть, но имеются поля и без камней (2 вида) , почвы бывают легкие, средние и тяжелые (3 вида), гон тоже может быть короткий, средний и длинный (3 вида). Следовательно, любое поле хозяйства может обладать совершенно определенными признаками по рельефу, каменистости, почве и длине гона.

В приведенном случае мы располагаем комбинациями (соединениями) из четырех элементов, где 2 элемента имеют по 2 разновидности и 2 — по 3, что можно записать так: элемент а имеет цифровые индексы 0 и 1, Ь — 0 и 1, с — 0; 1; 2 и

d — 0; 1; 2. Максимальное число различных по содержанию вариантов полей в данном случае составит 36, т.е. 2х2х3х3.

Наглядно это можно проследить по группировке множеств (рис. 5).

Определение общего количества всевозможных вариантов не представляет трудностей. Значительно сложнее бывает свести многочисленные объекты в группы, имеющие одни и те же признаки элементов.

Если элементов не много, а числа их делений малые, то, предварительно составив таблицу вариантов, можно довольно быстро отыскать номер (место) объекта в таблице. Но с возрастанием числа элементов и числа делений элементов сделать эту работу без помощи вычислительной техники становится почти невозможно. Достаточно указать, что при числе элементов 6 и при делении каждого из них на 4 части количество вариантов составляет 4096 (4⁶ = 4096). Кроме того, в практике (как и в нашем примере с полями) элементы имеют неодинаковое число делений.

Возникает необходимость в методе, позволяющем быстро и без помощи сложной техники разделить объекты при большом количестве как самих элементов, так и их делений на группы, имеющие одинаковые признаки.

Существует закономерность, согласно которой число и место вариантов находится при помощи коэффициентов, т.е. множителей индексов элементов.

Вернемся к примеру с полями. Запишем элементы с указанием наибольшего числа делений (индексов и). Это а Ь

с^, d^. В целях упрощения условимся впредь не писать букв обозначения элементов, оставив только цифровые значения индексов и помня, что на первом месте всегда находится первый элемент (а ), на втором — второй (Ь) и т.д. Тогда запись индексов в нашем примере будет выглядеть так: 1; 1; 2; 2.

Закономерность гласит, что если цифровые значения индексов попарно перемножить на коэффициенты 1; 2; 4; 12, то их сумма будет только на единицу меньше общего количества вариантов, т.е. 35.

(1х1) + (1х2) + (2х4) + (2х12) = 35. Как же были получены упомянутые коэффициенты? Если все элементы (кроме последнего делятся на 2, т.е. все элементы имеют величину индекса 1, то коэффициентами (/ ) является ряд чисел арифметической прогрессии 1; 2; 4; 8;

16; ... Последний элемент может иметь любое число делений. Это не влияет на величину его коэффициента.