Лекция I
ПРОЕКТИРОВАНИЕ ДОРОГ ДЛЯ ДВИЖЕНИЯ ТРАНСПОРТНЫХ ПОТОКОВ КАК ПУТЬ ПОВЫШЕНИЯ ЭФФЕКТИВНОСТИ РАБОТЫ АВТОМОБИЛЬНЫХ ДОРОГ
I. 1. СЛУЧАЙНЫЙ ХАРАКТЕР ФОРМИРОВАНИЯ ТРАНСПОРТНЫХ ПОТОКОВ НА АВТОМОБИЛЬНЫХ ДОРОГАХ
Автомобильная дорога и происходящее на ней движение потоков автомобилей представляют сложную композицию случайных явлений, изменяющихся как в пространстве, так и во времени. Случайно по длине дороги изменяются как элементы дороги, так и все характеристики движения автомобилей. Это вызвано случайной комбинацией форм рельефа, постоянными случайными изменениями климатических условий, участием человека в транспортном процессе, случайном характером выезда автомобилей на дорогу, т. е. случайным характером всех факторов, влияющих на формирование потоков автомобилей (рис. I. 1). Под воздействием этих факторов случайно меняются характеристики движения транспортных потоков: интенсивность, состав и скорости движения, ускорения, траектории и др.
На примере скорости и плотности движения можно проследить случайный характер их изменения во времени в одном сечении дороги (рис. 1.2). Движение автомобиля происходит по дороге, имеющей случайное распределение размеров и сочетаний элементов продольного профиля и плана. Это распределение в основном определяется рельефом местности, по которой проложена трасса дороги. Проведенные наблюдения за скоростями движения на ряде дорог показали существенное влияние комбинации элементов плана и продольного профиля на средние скорости движения на участке дороги (рис. 1.4). Скорости определяли по времени прохождения автомобилями исследуемого участка
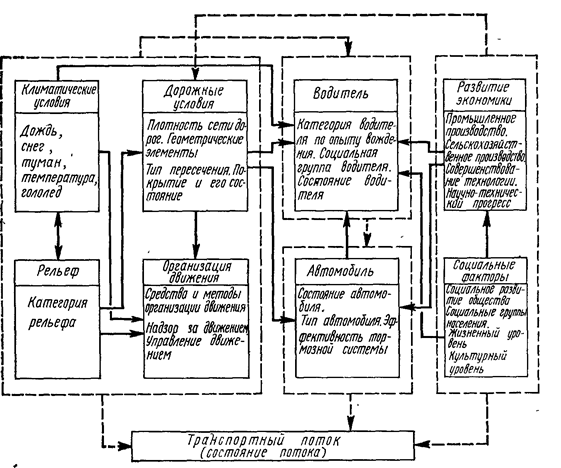
Рис. 1.1. Факторы, влияющие на формирование транспортных потоков
дороги, при этом регистрировали номерные знаки автомобилей. Изменение плана и продольного профиля дороги можно рассматривать как две случайные функции, от которых зависит третья случайная функция — функция изменения скорости вдоль дороги
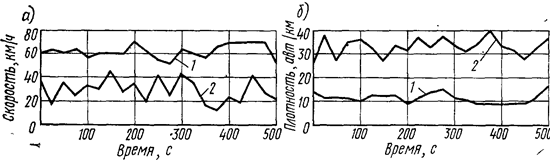
Рис. 1.2. Изменение во времени:
а — скорости движения; б — плотности движения;
1 — слабо пересеченная местность; 2 — сильно пересеченная местность
или других характеристик транспортного потока. Кроме того, на величину скорости оказывает влияние наличие человека — водителя, что вызывает случайные колебания скорости — «шум» скорости. Обычно водитель стремится выдержать желаемую скорость движения, которую он выбирает в зависимости от дорожных условий и расстояния до конечного пункта поездки. Однако при движении даже по горизонтальному участку дороги происходят отклонения от желаемой скорости. Такие отклонения вызваны: изменениями сопротивления качению, сопротивлением воздуха, невозможностью водителем выдерживать скорость постоянной и другими факторами. Эти отклонения также представляют чисто случайный процесс, который можно отнести к стационарным случайным процессам [17].
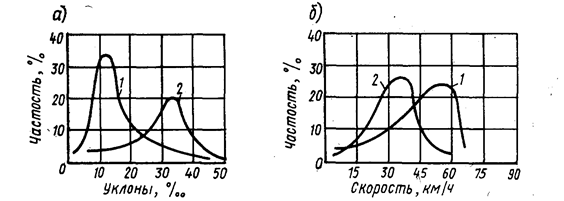
Рис. 1.4. Влияние статистических характеристик продольного профиля на статистические характеристики скорости движения:
а — распределение величин продольных уклонов; б — распределение величин скоростей движения;
1— слабо пересеченная местность; 2 — сильно пересеченная местность
На этот процесс накладывается влияние изменения скорости, вызванное продольным профилем и планом.
|
|
Для анализа случайных характеристик может быть использовано понятие о случайных функциях, известное из теории вероятностей [17]. Все указанные выше функции связаны между собой, поэтому можно использовать математический аппарат, позволяющий определять характеристики одной случайной функции
по характеристикам другой.
Рис. 1.5. Пример корреляционной функции продольного
профиля
Случайная функция характеризуется тремя показателями: математическим ожиданием тх (t), дисперсией Dх(t) и корреляционной функцией Кх(t,t). Зная эти показатели для одной случайной функции, можно определять такие же показатели для другой функции. Заданными функциями можно считать, случайные функции изменения продольного профиля и плана. На основе этих функций может быть, например, определена функция скорости.
Если рассмотреть случайную функцию изменения координат продольного профиля, то можно отметить, что ее параметры определяются размерами элементов рельефа местности и изменяются по длине l. Математическое ожидание тi(1) и дисперсию Di (l) можно определить непосредственно на основе координат положения проектной линии. Характеристикой степени колебания функции продольного профиля является корреляционная функция Кi(1,l`), показывающая степень связи между соседними значениями координат продольного профиля х(1) и х(l`). Часто используют нормированную корреляционную функцию
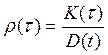 (1.1)
(1.1)
где ![]() .
.
На рис. 1.5 показан пример изменения
нормированной корреляционной функции ![]() для неблагоприятного
продольного профиля с малыми радиусами вертикальных кривых, аппроксимируемой
полиномом [66]:
для неблагоприятного
продольного профиля с малыми радиусами вертикальных кривых, аппроксимируемой
полиномом [66]:
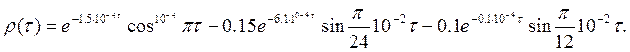 (1.2)
(1.2)
На основе этой функции продольного профиля можно определить средние характеристики изменения скорости движения mv(t)=42 км/ч; Dv(t)=37 км2 /ч2; σ=6,09 км/ч.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.