Проектирование дорог для движения транспортных потоков как путь повышения эффек­тивности работы автомобильных дорог. Взаимодействие автомобилей в транспортном потоке. Макроскопические теории транспортного потока, страница 34

От правильности выбора закона распределения интервалов между поступлением событий (автомобилей) зависит точность и досто­верность получения конечных результатов. Ниже будут рассмот­рены законы распределения, которые могут быть использованы для описания характеристик движения потока автомобилей, как вероятностного процесса, в котором появление одного авто­мобиля не связано с моментом появления впереди идущего ав­томобиля, а величины соседних интервалов не имеют корреляци­онной связи. Последнее предположение не совсем справедливо для реальных условий движения, так как на движение автомо­билей существенное влияние оказывают дорожные условия, раз­нородность состава движения, а также взаимное влияние авто­мобилей, движущихся при высоких скоростях.

Дискретные распределения. К дискретным распределениям относятся: распределение Бернулли, биноминальное и отрица­тельное биноминальное распределения,   гипергеометрическое распределение, распределение Пуассона и др. Характеристики этих распределений приведены в табл. 111.1.

Распределение Бернулли показывает вероят­ность появления р или отсутствия q = 1 — р события:

Р (х/р) = р^х q ^1-х                                                                                                                                                                             (111.1)

Биноминальное распределение является первым основным уравнением теории вероятностей и показывает распре­деление числа m появлений событий при п независимых испы­таниях, при каждом из которых вероятность появления события р остается постоянной. Вероятность отсутствия события q=1-р. Общий вид уравнения следующий:

P_n,m = 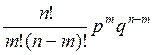.                                                                                          (III.2)

Отрицательное биноминальное   распределе­ние является разновидностью биноминального распределения, и оно показывает вероятность необходимости проведения х наб­людений до появления k событий. Каждое событие появляется с вероятностью р. Вид этого распределения следующий:

.                                                                                           (111.3)

Гипергеометрическое   распределение   имеет место, когда из N каких-либо событий М событий обладает каким-либо свойством А и необходимо вычислить вероятность того, что т событий обладает свойством А, а п—т не обладают. Распре­деление имеет вид:

P_m = 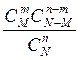.                                                                                                                                                    (III.4)

Распределение Пуассона наиболее широко приме­няется в теории вероятностей и особенно в теории массового обслуживания. Оно имеет вид:

P_n(t) = e^-λt 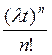                                                                                                                             (III/5)

Это уравнение показывает вероятность появления п событий, поступающих с интенсивностью λ в интервале времени (0, t). Это уравнение широко применяется в теории  транспортных по­токов.

Непрерывные распределения. К непрерывным распределениям относятся: нормальное распределение, распределения Граме-Шарлье, Вейбулла, Максвелла, Парето, Пирсона, Эрланга, гам­ма- и бета- распределения, распределения смеси, экспоненциаль­ное (показательное) и гиперэкспоненциальное распределения и др. Статистики непрерывных распределений приведены в табл. 111.2.