Проектирование дорог для движения транспортных потоков как путь повышения эффек­тивности работы автомобильных дорог. Взаимодействие автомобилей в транспортном потоке. Макроскопические теории транспортного потока, страница 41

К смешанным распределениям, можно также отнести уравне­ния, описывающие отдельные ветви кривых распределения. Примером такой зависимости является уравнение (111.41) и уравне­ние, полученное В. В. Филипповым [56]:

                                            P(Δt) = 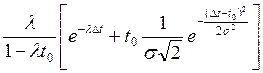 ,                                              (III.41)                                

где λ — параметр потока, авт/с; t₀ — среднее время прохождения автомоби­лем расстояния, равного средней величине динамического габарита;  σ — сред­нее квадратическое отклонение величин интервалов в стесненной части потока.

В уравнении (III. 41) первый член в скобках описывает экспо­ненциальную часть кривой, второй — область малых интервалов.

Анализ смешанных распределений показал, что они имеют тот же недостаток, что и экспоненциальные распределения, которые характерны для потоков автомобилей низкой плотности. Этот класс распределений имеет следующую область применимости: на дорогах с двумя полосами движения до 450 авт/ч: на автомагист­ралях с четырьмя полосами движения до 1000 авт/ч, на автомаги­стралях с шестью полосами движения до 2000 авт/ч (рис. 111.11).

Применение этих законов распределения несомненно усложня­ет аналитический аппарат, поэтому перспективным является их использование при моделировании транспортных потоков на компьютерах.

Применимость распределения Пирсона III типа. Это распреде­ление наиболее близко по форме фактическому распределению ин­тервалов во времени (рис. III. 11). Анализ этого распределения показал, что оно применимо: на дорогах с двумя полосами движе­ния до 650 авт/ч, на автомагистралях с четырьмя полосами дви­жения — до 1250 авт/ч, на автомагистралях с шестью полосами движения — до 2250 авт/ч.

Применимость распределения Эрланга. Это распределение мо­жет быть применено как для описания распределения интервалов во времени, так и по длине. Анализ этого распределения показал,

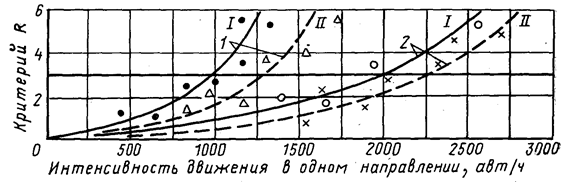
Рис. 111.11. Применимость смешанного распределения и распределения Пирсона III типа (по данным А. Н. Красникова):

1 — четырехполосная автомагистраль; 2 — шестиполосная автомагистраль;

/ — смешанное распределение; // — распределение Пирсона III типа

что оно применимо на двухполос­ных дорогах до 300 авт/ч, на ав­томагистралях с четырьмя поло­сами движения до 800 авт/ч и на автомагистралях с шестью поло­сами движения до 1200 авт/ч.

Применимость гамма-распре­деления. Это распределение до­статочно эффективно может быть использовано для описания рас­пределения интервалов во време­ни на автомагистралях (рис. III.12).

В табл. 111.6 приведены обла­сти применимости всех перечис­ленных выше распределений. Из таблицы видно, что распределе­ние Пуассона применимо при уровне удобства движения А, а остальные распределения — при уровне удобства Б.

Практические задачи, решаемые с помощью вероятностных мо­делей. Результаты оценки применимости вероятностных моделей показывают, что эти модели являются основными для теоретиче­ского описания движения потока автомобилей низкой плотности (при z ≤ 0,5). Такое состояние потока наиболее характерно и тре­бует разработки различных мероприятий по повышению безопас­ности и удобства движения. Причем эти мероприятия могут быть как планировочными, так и относящимися к организации движения. С помощью вероятностных моделей   можно решать следую­щие группы задач (рис. 111.13): оценку эффективности планировоч­ных решений и средств регулирования; оценку пропускной способ­ности участков пересечения, переплетения и слияния потоков автомобилей; выбор оптимального режима управления движением с помощью светофоров; оценку аварийности; оценку эффективности работы системы обслуживания на дорогах (стоянок, площадок от­дыха, автозаправочных станций и т. п.).

Таблица 111.6