Безопасность жизнедеятельности \ Теория транспортных потоков

Проектирование дорог для движения транспортных потоков как путь повышения эффек­тивности работы автомобильных дорог. Взаимодействие автомобилей в транспортном потоке. Макроскопические теории транспортного потока, страница 37

Таблица III. 3

Характеристика потока

Расчетные формулы

Вероятность нахождения n автомобилей на данном участке дороги рn

Вероятность нахождения более n автомобилей на данном участке дороги р ( n ≥ n∑ )

Средняя длина очереди n`, включая обслуживае­мый автомобиль

Средняя длина очереди n0 (без учета обслужива­емого автомобиля)

Среднее число автомобилей, задержанных в оче­реди n*0

 

Дисперсия n0, var[n0]

 Вероятность времени tc нахождения автомобилей на данном участке в рассматриваемой системе мас­сового обслуживания р (tc)

Среднее время нахождения автомобиля на данном участке tc tc (например, ожидание в очереди и обгон)

Среднее время ожидания в очереди tож

Вероятность затраты времени t или менее на дан­ном участке дороги р (tc ≤ t)

 Вероятность ожидания в очереди времени t или менее p(t0≤t)

Pn = (1-z)zn

Pn ≥ n∑  = zn+1

no =

var [n0] = z / (1-z)2

 

р (tc) = (P – N) e(P-N)tC

 

tc = 1 / (P – N)

tож = N / p (P-N) = tc – P-1

p(tc ≤ t) = 1 – e-(1-z)Pt

 

p(tc ≤ t) = 1 – ze-(1-z)Pt

Примечание, z — коэффициент загрузки; Р—пропускная способность полосы движения;

N—интенсивность прибывающего потока автомобилей.

Вероятности состояний системы массового обслуживания мо­гут быть вычислены по формулам:

p1 = (N/P) p0 = zp0;

p2 = (N/P)2 p0 = z2 p0;

………………………

pk = (N/P)k p0 = zk p0;                                                                                                                       (III.18)

      ………………………

pn+1 = (N/P)n+1 p0 = zn+1 p0;

p0 = .

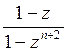Вероятность отказа ротк системы определяется по формуле

ротк = pn+1 = 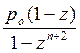.                                                                                    (III.19)

Число автомобилей, находящихся в очереди,

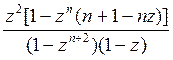   n0 = .                                                                                             (III.20)

Среднее число обслуживаемых автомобилей

                                                   nобс = 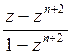                                                                                          (III.21)

Среднее время ожидания автомобиля в очереди

                                                         tожд = 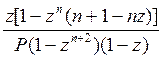.                                                            (III.22)

При эрланговском [см. уравнение (111.17)] времени обслужива­ния (случай II), что характерно для более уплотненных потоков автомобилей, формулы для расчета характеристик ожидания ме­няются (табл. 111.4).

Многоканальная система с ожиданием (случай III) может быть применена для получения характеристик образования оче­редей на участках изменения числа полос движения.

Таблица III.4

Характеристики потока

Pасчетные формулы

Среднее число автомобилей на данном участке п

Средняя длина очереди no

Среднее время нахождения автомобиля на данном участке

Среднее время ожидания в очереди to

n0 =

tc =

t0 =

Расчетные формулы для случая, когда длина очереди не ог­раничивается, представлены в табл. 111.5.

При расчетах, связанных с организацией движения в зоне авто­заправочных станций, станций технического обслуживания или придорожных ресторанов необходимо рассматривать случаи с ог­раниченной длиной очереди: в первом случае ограничение места для очереди автомобилей с тем, чтобы она не выходила на основ­ную проезжую часть, во втором случае ограничение емкости обо­рудованной стоянки перед рестораном. Для этого могут быть ис­пользованы следующие формулы:

вероятность отказа

                                                     ротк = pn+m = 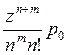;                                                                    (III.23)

                            p0 = 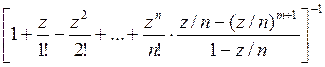;                                              (III.24)

среднее число занятых каналов

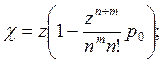                                                                                                                         (III.25)

среднее число автомобилей в очереди

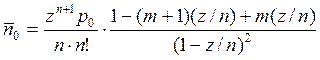                                          ;                                          (III.26)

Скачать файл