Проектирование дорог для движения транспортных потоков как путь повышения эффек­тивности работы автомобильных дорог. Взаимодействие автомобилей в транспортном потоке. Макроскопические теории транспортного потока, страница 46

       v_n+1 = v_n +t_p,

Или

 v_n+1 – v_n = t_p ,

Или

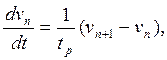                                                                 (IV.7)

где    — ускорение заднего автомобиля; v_n и v_n+1  — скорости заднего и переднего автомобилей; t_p — продолжительность реакции водителя.

Уравнение (IV.7) является первым дифференциальным уравне­нием теории «следования за лидером». Полученное правило может быть сформулировано следующим образом: при следовании двух автомобилей друг за другом на достаточно близком расстоянии, когда оказывается их взаимное влияние, ускорение  зад­него автомобиля прямо пропорционально раз­ности скоростей переднего и заднего автомо­билей (относительной скорости). Это основной и наиболее простой закон теории «следования за лидером».

Дробь  обычно обозначают буквой α и называют коэффи­циентом пропорциональности или чувствительностью водителя. Учитывая это, перепишем уравнение (IV.7) в следующем виде:

                                                          = α(v_n+1 – v_n).                                                                   (IV.8)

Следовательно, основной принцип модели «следования за ли­дером» состоит в том, что -водитель реагирует главным образом на раздражение, поступающее из окружающей среды (воздействие), в соответствии с соотношением:

(Реакция) t + t_p = α (Воздействие)

В данном случае реакцией является ускорение, изменяемое во­дителем с помощью тормозов и акселератора, а воздействие — разность скоростей переднего и заднего автомобилей.

Дальнейшие исследования показали, что величина коэффициен­та α зависит от расстояния между автомобилями. Д. Гейзис, Р. Герман и Р. Потc [107] предположили, что показатель чувстви­тельности водителя α обратно пропорционален расстоянию между автомобилями:

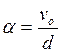,                                                                    (1У.9)

где v_o — характерная скорость;  d — расстояние между автомобилями.

В результате было получено второе основное уравнение тео­рии «следования за лидером»:

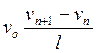 = .                                                          (1У.10)

Этот закон «следования за лидером» можно выразить так:

ускорение заднего автомобиля прямо пропор­ционально разности скоростей переднего и зад­него автомобилей и обратно пропорционально расстоянию между ними.

Аналогичное уравнение было предложено Л. Эдаем [104], ко­торый исходил из предположения, что чувствительность водителя изменяется с изменением скорости движения: чем выше скорость движения, тем выше чувствительность водителя. Чувствительность также обратно пропорциональна расстоянию между автомобиля­ми; если передний автомобиль очень близко, то чувствительность выше. На основе этих предположений была предложена следую­щая зависимость:

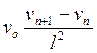                                                                    = α₂.                                                   (IV.11)

В этом уравнении чувствительность принята обратно пропор­циональной величине интервала во времени между двумя автомо­билями, так как водитель заднего автомобиля с уменьшением про­межутка времени становится более внимательным. Величина ин­тервала во времени равна l/v_n. В уравнении (IV.II) показатель чувствительности водителя равен

α = 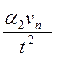                                                                                               (1У.12)

При детальном рассмотрении тенденции изменения зависимо­сти α от различных факторов было получено общее выражение для определения величины чувствительности:

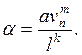                                                                                (IV.13)

Учитывая уравнения (IV.11) и (IV.13), получаем уравнение теории «следования за лидером» в общем виде

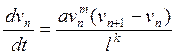                                                                            (1У.14)

Г. И. Клинковштейн, В. Б. Ботцманов и С. В. Норкин [117] предложили уравнение теории «следования за лидером» в следую­щем виде

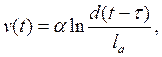                                                                                                                                 (1У.15)

где v(t) — скорость ведомого автомобиля; lа — длина расчетного автомобиля;

d — дистанция между автомобилями, м.