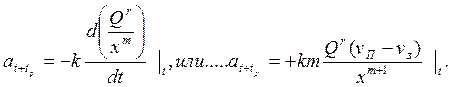Проектирование дорог для движения транспортных потоков как путь повышения эффек­тивности работы автомобильных дорог. Взаимодействие автомобилей в транспортном потоке. Макроскопические теории транспортного потока, страница 48

                                                   (IV.18)

В этом случае, чем меньше расстояние между автомобилями и чем больше площадь переднего, тем больше замедление заднего автомобиля.

При движении автомобилей в колонне расстояние между авто­мобилями непрерывно изменяется.

Водитель выбирает моменты времени, в которые необходимо из­менить ускорение своего автомобиля с тем, чтобы установилось оптимальное, с его точки зрения, расстояние до переднего автомо­биля.

Этот момент возникает, когда расстояние между автомобилями становится равным Со+ Δd₁ или

Со -Δd₂, где Δd₁ и Δd₂— измене­ние расстояния между автомобилями соответственно при разгоне и торможении переднего автомобиля.

Применение предложенной аналитической модели, учитываю­щей габариты впереди идущего автомобиля, позволяет учитывать состав движения в плотном потоке автомобилей.

Устойчивость движения колонны автомобилей. При исследова­нии режима движения колонн автомобилей большое значение имеет анализ устойчивости всех характеристик движения ко­лонны.

Основой этого анализа является математическая теория устой­чивости [17].

Под устойчивостью будем понимать способность ка­кой-либо характеристики режима движения автомобилей в колон­не (например, скорости), сохранять свое начальное значение во времени.

В случае если величина характеристики приближается со временем к начальному значению, то такую устойчивость на­зывают асимптотической устойчивостью.

Локальная устойчи­вость характеризует отно­сительное положение задан­ной пары автомобилей, а асим­птотическая—затухание или усиление амплитуды возмуще­ний при распространении их вдоль колонны автомобилей (рис. IV.9)

Отмечено [11О], что локальная устойчивость зависит от произ­ведения v_o t_p. Если v_o t_{p ≤} 1/e, то возмущение монотонно затухает (е=2,72—основание натурального логарифма). Если 1/е ‹ v_o t_{p ≤} π/2, то возмущение вызывает затухающие колебания расстоя­ния между автомобилями.

Если v_o t_{p ›} π/2, то возмущение вызывает колебания, амплитуда которых возрастает с течением времени.

Асимптотическая устойчивость исследовалась путем рассмотре­ния синусоидального возмущения скорости бесконечной колонны автомобилей. Оказалось, что в наиболее критической области — об­ласти низких частот—амплитуда увеличивается или уменьшается в зависимости от того, больше или меньше '/2 значения v_o t_p, т. е. колонна автомобилей может быть локально устойчивой, а асимпто­тически неустойчивой.

IV. 4. СПЕКТРАЛЬНАЯ ТЕОРИЯ  ВЗАИМОДЕЙСТВИЯ АВТОМОБИЛЕЙ В КОЛОННЕ

Движение потока автомобилей в режиме следования за лиде­ром — типичный пример случайной системы. Случайными взаимо­действующими функциями в этом случае являются: функция изме­нения во времени скорости переднего автомобиля и функция из­менения во времени скорости заднего автомобиля. Одновременная запись этих двух функций в реальных условиях может быть осу­ществлена по тому же принципу, что и регистрация времени реак­ции водителя [39]. В данном случае радиосигналы с переднего ав­томобиля несут информацию о скорости. В заднем автомобиле осу­ществляется одновременная запись скоростей обоих автомобилей. Таким методом можно изучать связь функций скоростей передне­го автомобиля и любого по счету автомобиля в колонне.

Учитывая, что обе эти функции случайны, для их анализа мо­жет быть успешно применена теория случайных функций (спект­ральный анализ). Основными показателями взаимодействия авто­мобилей являются:

автокорреляционная функция

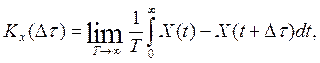                                                                                         (IV.19)

где Т — общий период наблюдений;

спектральная плотность (рис. IV. 10, а)

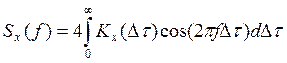                                                         (1У.20)

Для удобства часто использу­ют нормализованную автокорре­ляционную функцию

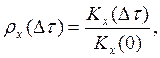                                                                                                                        (^1У-²¹)