Проектирование дорог для движения транспортных потоков как путь повышения эффек­тивности работы автомобильных дорог. Взаимодействие автомобилей в транспортном потоке. Макроскопические теории транспортного потока, страница 35

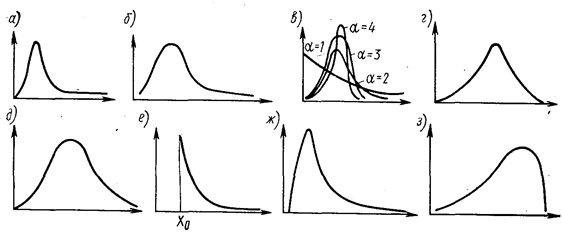
Рис. 111.2. Общий вид непрерывных распределений:

а — логарифмически нормального; б — Граме-Шарлье; в — Вейбулла;г — гамма-распреде­ления; д — Максвелла; е — Парето; ж — Пирсона I типа; з — Пирсона III типа

Нормальное распределение Лапласа — Гаусса имеет плотность, задаваемую уравнением

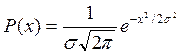,                                                                                                                                              (III.6)

где x = Х— — представляет собой отклонения от среднего значения; σ—ос­новное отклонение.

Логарифмически нормальное распределение (рис. III.2,а) имеет плотность, выражаемую уравнением

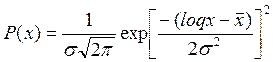.                                                                                            (III.7)

Кривая распределения Граме-Шарлье, тип А (рис. 111.2,б), является обобщением нормального распределения и распределения Пуассона:

f_А(x) = f (x) - f⁽³⁾ (x) + 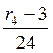f⁽⁴⁾ (x),                                                                                             (III.8)

где                               f (x) = ;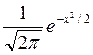                                  

f⁽³⁾ (x)   = - (x³ – 3 x) f (x);                       f⁽⁴⁾ (x) = (x⁴ – 6 x² + 3) f (x)

r – основные моменты распределения [33].

Кривая распределения   Г р а м е-Ш а р л ь е, тип В (рис. 111.2,6), также получена на основе функции распределения Пуассона и имеет вид

f_В(x) = ,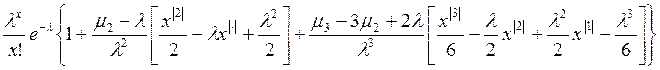

где μ — центральные моменты распределения;    —число событий в интерва­ле значений   .                                  (III.9)

Распределение Вейбулла (рис. III.2,б) имеет вид

Р(х) =1—е^-cxα при х>0,                   (111.10)

где с и α — положительные параметры.

Гамма-распределение (рис. Ш.2,г) имеет плотность, задаваемую уравнением

f (x)  = C x ^α-1 e^-βx    ,                                                                                                                                                          (111.11)

где

С = ;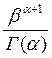

Г(α) = ;

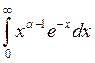α > 0;   β > 0 — постоянные распределения.

Бета-распределение имеет плотность:

f (x) = 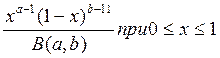,                                                                                           (III.12)

где В(a,b) = .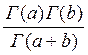

Распределение смеси имеет место, когда случайная ве­личина является смесью двух или более случайных величин с раз­личными распределениями. Это распределение наиболее харак­терно для транспортного потока.

Распределение Максвелла (рис. II. 2, д) имеет плотность, задаваемую выражением

P(x) = 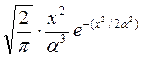,                                                                                                                 (III.13)

Распределение Парето (рис. III. 2, е) имеет плот­ность

P(x) = 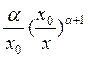,                                                                                                                                        (III.14)

где x₀ — наименьшее значение исследуемого признака: x ≥ x₀;  α › 0.

Экспоненциальное   (показательное) распре­деление является фундаментальным в теории массового обслу­живания, описывающим время обслуживания:

Р(х)= λe^-λx ; λ >0.                   (111.15)

Гиперэкспоненциальное распределение имеет плотность

P(x) a₁λ₁e^-λ₁^x + a₂λ₂ e^-λ₂^x + … + a_кλ_к e^-λ_к^x   ,                                                                                                                           (111.16)

 где а — вероятность отдельных составляющих.

В табл. 111.2 даны статистики этого распределения как одного из вариантов распределения смеси, но только состоящей из пока­зательных распределений.

Распределение Пирсона I и III типа (рис. III. 2, ж, з) широко применяют в теории транспортных потоков.

Распределение Эрланга имеет широкое применение в теории вероятностей. Функция распределения имеет вид

                                      P (q ≥ t) = 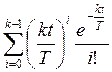,                                                                               (III.17)

где k > 0 — параметр распределения.

Приведенные выше законы распределения охватывают практи­чески все возможные кривые распределения, которые могут встре­чаться при изучении характеристик движения транспортного по­тока. Однако необходимо иметь в виду, что они получены при уп­рощенном толковании потока случайных событий. Поэтому необ­ходима детальная проверка возможности применения этих рас­пределений для описания движения потоков автомобилей.