Проектирование дорог для движения транспортных потоков как путь повышения эффек­тивности работы автомобильных дорог. Взаимодействие автомобилей в транспортном потоке. Макроскопические теории транспортного потока, страница 43

Большое значение имеет установление связи между автомоби­лями, движущимися друг за другом, т. е. установление законо­мерности передачи возмущений, создаваемых передним автомоби­лем на задний автомобиль.

Микроскопический подход особенно эффективен при решении задач, связанных со сравнительно короткими участками дорог.

Макроскопический подход. Этот подход основан на предпола­гаемой аналогии между движением потока автомобилей и сплош­ной среды (сжимаемой или несжимаемой жидкости) и примене­нии математического аппарата, используемого в гидродинамике или газодинамике. Такой способ позволяет получать только общие характеристики движения потока автомобилей как сплошной сре­ды (плотность, интенсивность, скорость, энергетическое состояние). Поэтому практическим результатом такого подхода является полу­чение связей между этими общими характеристиками. Процессы, происходящие внутри потока, в этом случае не могут быть иссле­дованы достаточно детально. Практическое значение имеет анализ волнового движения потока автомобилей с точки зрения выявления степени влияния препятствий.

IV. 2. ДИНАМИЧЕСКАЯ ТЕОРИЯ ДВИЖЕНИЯ ПЛОТНОГО ПОТОКА АВТОМОБИЛЕЙ

Взаимодействие между автомобилями в плотном транспортном потоке, зависящее от действий водителей, в первую очередь, прояв­ляется в изменении дистанции между автомобилями. Поэтому пер­вые упрощенные динамические теории были разработаны с целью возможности расчета средней дистанции между автомобилями при различных скоростях движения.

Все упрощенные динамические модели основаны на предполо­жении, что автомобили движутся в колонне с одинаковой ско­ростью на расстоянии, достаточном для полной остановки без на­езда на впереди идущий автомобиль. Наиболее полная оценка уп­рощенных динамических уравнений с точки зрения определения пропускной способности дана в работах М. С. Фишельсона, В. А. Юдина, Ю. С. Крылова и Л. А. Кероглу.

Можно выделить несколько групп упрощенных динамических моделей, основанных на различных начальных предпосылках:

1-я группа—уравнения, в которых не учитывается тормозной путь (В. Швантер, Б. Гриншильдс, Ю.М. Даденков и др.);

2-я группа — уравнения, в которых учитывается полный тор­мозной путь (А. К. Бируля, Ю.С.Крылов, Г. Бергман, Р. Шаар и др.);

3-я группа — уравнения, в которых учитывается разница в тормозных путях заднего и переднего автомобилей (М. С. Фи-шельсон, А. А. Поляков, Д. Аллен, Д. П. Великанов и др.);

4-я группа—уравнения, полученные в результате статистиче­ской обработки данных наблюдений за расстоянием между автомобилями при различных скоростях движения (Н. Ф. Хорошилов, В. А. Юдин, В. М. Трибунский и др.).

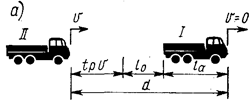
Рис. IV.!.  Зависимость интервалов по длине от скорости движения на основе уравнений 1й группы:

а — расчетная схема движения; б — гра­фик зависимости минимального интерва­ла по длине от скорости;

1 — по данным Б. Ю. Гуревича;  2 — Ю. М. Даденкова; 3 — Д. Иоганнесона;

4—Б. Гриншнльдса; 5—В. Швантера

Общий вид уравнений 1-й группы имеет вид

                                                              d = l_a + l_p + l_o,                                                                              (IV.1)

где d — минимальное безопасное расстояние между автомобилями (динамичес­кий габарит автомобиля), м; /а — длина автомобиля, м; 1о — запас пути, м; l_p — путь, проходимый задним автомобилем за время реакции водителя, м.

Анализ уравнений этой группы показывает (рис. IV.!) большое различие величины, расстояния между автомобилями, получаемого по этим уравнениям, вызванное различием величины времени ре­акции. Основной недостаток этой группы уравнений — отсутствие учета в них тормозных качеств автомобилей и сцепления шины ко­леса автомобиля с покрытием дороги.

В уравнениях 2-й группы учитывается полный тормозной путь заднего автомобиля при внезапной остановке переднего. Эти урав­нения имеют следующий вид (рис. 1У.2):

d = l_a +l_T  + l_p + l_o                                                                              (1У.2)