где Кх(0) — значение автокорреляционной функции при начальных условиях.
Автокорреляционная функция постепенно приближается к нулю (рис. IV. 10, б), показывая, что функции скоростей некоррелируются и что частотная составляющая функция скорости в основном имеет низкую частоту, около 1,5 колеб./с. Это также видно из рис. IV. 11.
Для одновременного качественного описания функций скоростей обоих автомобилей могут быть использованы [107]: взаимная корреляционная функция, взаимная спектральная плотность, функция когерентности.
Взаимно - корреляционная функция Кху(t) описывает зависимость одной функции скорости от другой:
К xy(t) = 
,
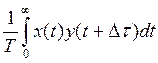(1У.22)
На рис. IV.11 показана нормализованная взаимно-корреляционная функция, существующая между функциями изменения скорости переднего и заднего автомобилей. Эта функция отложена в зависимости от времени запаздывания в колонне автомобилей. Максимальную величину эта функция имеет при t=14с.
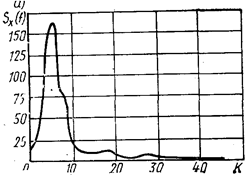
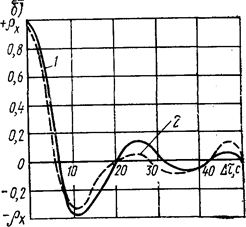
Рис. IV. 10. Функции, характеризующие случайное взаимодействие автомобилей, движущихся в режиме следования за лидером:
а — спектральная плотность; б — автокорреляционная функция; ; — передний
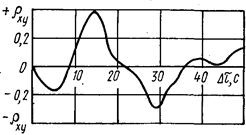
Рис. IV. 11. Взаимно автокорреляционная функция
|
|
|
Рис. 1У.12. Функция когерентности: к—номер волны |
Взаимная спектральная плотность вычисляется по формуле
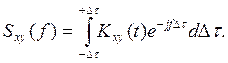(1У.23)
Функция когерентности 
имеет вид
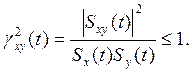(IV.24)
Эта функция
показывает связь двух функций (в рассматриваемом случае функций изменения
скорости во времени переднего и следующего за ним автомобиля). Независимость
функций имеет место при = 0, полная связь
при = 1. Функция когерентности уменьшается с
ростом номера волны (рис. 1У.12).
Применение описанного математического аппарата теории случайных функций позволяет более детально исследовать взаимодействия внутри колонны автомобилей. Особый интерес представляют уравнения (IV. 19) — (1У.21), используемые для оценки распространения возмущения внутри колонны автомобилей, определения расстояния в колонне, на которое распространяется возмущение, и определения оптимальной длины колонны автомобилей. Большие возможности открывает применение теории обратной связи.
Лекция 7
IV. 5. МАКРОСКОПИЧЕСКИЕ ТЕОРИИ ТРАНСПОРТНОГО ПОТОКА
Наряду с динамическими моделями, описывающими движения и взаимодействие отдельных автомобилей, возможна разработка теоретических моделей, позволяющих дать общую оценку макроскопических явлений, происходящих в потоке автомобилей [100, 115], который рассматривается как сплошная среда, состоящая из большого числа близко расположенных друг к другу автомобилей. Для математического описания состояния движущегося потока автомобилей как сплошной среды необходимо использовать следующие основные законы: уравнение состояния потока автомобилей; уравнение неразрывности; закон сохранения количества движения; закон сохранения энергии. Рассмотрим основные уравнения для движения потока автомобилей высокой плотности.
Уравнение состояния потока автомобилей. Под уравнением состояния потока автомобилей как сплошной среды понимают уравнение, связывающее между собой интенсивность N. плотность q и скорость v движения потока автомобилей,
N= qv. (1У.25)
Уравнение неразрывности. Это уравнение основано на принципах закона сохранения масс. При анализе потока автомобилей рассматривается постоянство общего числа автомобилей во времени, т. е. dn/dt = 0. Изменение общего числа автомобилей на участке дороги dS может происходить как в результате изменения плотности q, так и в результате изменения интенсивности. Этим объясняются две составляющих в уравнении (IV. 26).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
