Проектирование дорог для движения транспортных потоков как путь повышения эффек­тивности работы автомобильных дорог. Взаимодействие автомобилей в транспортном потоке. Макроскопические теории транспортного потока, страница 53

По диаграмме «интенсивность-плотность» можно определить все характеристики движения потока автомобилей: скорость, плот­ность, интенсивность, скорость распространения ударной волны и т. д. (см. рис. IV. 13). Часть кривой, расположенная слева от линии I—I, соответствует нормальным условиям движения без образова­ния заторов, правая кривая—движению автомобилей при возник­новении заторов. По этой зависимости средняя скорость движения определяется как частное от деления интенсивности движения N (авт/ч) на плотность q (авт/км). Другими словами, тангенс угла наклона радиуса-вектора N/q равен средней скорости движения потока автомобилей. Максимальная интенсивность, получаемая по диаграмме, соответствует пропускной способности рассматривае­мого участка дороги. Тангенс угла наклона к оси х касательной к кривой «интенсивность—плотность» равен скорости распростране­ния волны в потоке автомобилей.

Кроме указанных характеристик движения потока автомобилей по диаграмме можно также оценить среднюю величину интервала во времени между движущимися друг за другом автомобилями Δt и интервала во времени между задним бампером переднего авто­мобиля и передним бампером заднего автомобиля δt. Эти показа­тели определяются по следующим уравнениям:

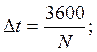                                                                                                                                           (IV.43)

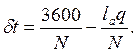                                                                                                                                 (IV.44)

Общий вид уравнения «интенсивность-плотность», полученного на основе уравнения теории «следования за лидером», следующий:

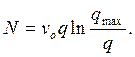                                                                                       (1У.45)

Это уравнение идентично с уравнением Д. Гринберга [104] при v₀ = С. В уравнении (1У.44) v₀—характеристическая скорость движения потока автомобилей на рассматриваемом участке доро­ги. Эта скорость получается на основе анализа взаимодействия двух движущихся друг за другом автомобилей на этом участке дороги.

Кривая «интенсивность — плотность» может быть также полу­чена с помощью уравнений 3-й группы упрощенной динамической теории движения потока автомобилей. Эту кривую строят на осно­ве решения динамического уравнения 3-й группы:

D=l_a + t_pv +Bv²;                                                                               (IV.46)

                                                        B = ½ (a_n+1 – a_n),

где a_n+1 — максимальное замедление (п +1)-го автомобиля; а_n — максималь­но возможное замедление n-го автомобиля.

Уравнение (1У.45) решается относительно скорости v. В ре­зультате получается

                                                                        (IV.47)

где                     q = 1/S;   q_max = 1/S_o;      α = t/l_a;      β = B/l_a.

Интенсивность движения определяют с помощью уравнения связи основных характеристик транспортного потока:

N =vq.

Отсюда общий вид зависимости «интенсивность-плотность», полученной на основе уравнения 3-й группы упрощенной динами­ческой теории, следующий:

                         ,                         (1У.48)

где N_o = αq_max / 2β;  γ = 4 β / α² .

После дифференцирования обеих частей уравнения (1У.48) по­лучаем

,                                                                                                               (IV.49)

или

.                                                                                                         (1У.50)

Уравнение (1У.50) может быть рассмотрено как уравнение теории «следования за лидером» с чувствительностью

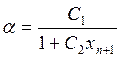.                                                                                        (IV.51)

Следовательно, несмотря на различный подход к выводу основ­ного уравнения движения транспортного потока, конечные резуль­таты всех динамических теорий (за исключением газовой) близки друг к другу.

Уточнение динамических теорий в настоящее время возможно только на основе проведения широких натурных наблюдений за движением транспортных потоков различных по составу и движу­щихся в различных дорожных условиях.