Проектирование дорог для движения транспортных потоков как путь повышения эффек­тивности работы автомобильных дорог. Взаимодействие автомобилей в транспортном потоке. Макроскопические теории транспортного потока, страница 38

среднее число автомобилей в системе

                                                                                                                                                  (111.27)

среднее время ожидания

                                             t_ож = 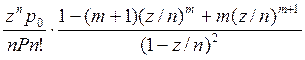;                                       (III.28)

среднее время пребывания в системе

                                           t_c = t_ож + 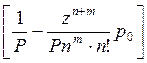.                                                                  (III.29)

Зависимости (111.23—111.29) пригодны для простейших, т. е. пуассоновских потоков. Эти потоки характерны для коэффициента загрузки z ≤ 0,3 и уровня удобства А и частично Б. В случае когда интенсивность достаточно высокая и резко меняется, эти за­висимости непригодны, так как поток значительно отличается от пуассоновского. Поэтому необходимо всегда анализировать обла­сти практического применения результатов, полученных на основе теории массового обслуживания решений.

111. 4. ПРИМЕНЕНИЕ ЦЕПЕЙ МАРКОВА В ТЕОРИИ ТРАНСПОРТНЫХ ПОТОКОВ

Для математического описания транспортного потока как слу­чайного процесса может применяться  математический аппарат, разработанный в теории вероятностей для марковских случайных процессов [17].

Под марковским процессом (процессом без последствия) пони­мается процесс, обладающий следующим свойством: для каждого момента времени t₀ вероятность любого состояния системы в буду­щем (при t > t₀) зависит только от ее состояния в настоящем (при t = t_o) и не зависит от того, когда и каким образом система пришла в это состояние.

Марковской цепью называют такую случайную последователь­ность событий, при которой в цепочке событий вероятность пере­хода из любого состояния S_i в любое S_j, не зависит от того, когда и как система пришла в состояние S_i. При этом изменение состоя­ний системы происходит в какие-то моменты: t₀, t₁, t₂ …, t_k.

Используют следующее обозначение события : S, состоящее в том, что после R шагов система находится в состоянии S_i; ве­роятность того, что в данный момент t система находится в со­стоянии S_i, обозначается р_i(t). При использовании цепей Маркова ставится задача определения вероятности нахождения системы в каком-либо состоянии.

Движение потока автомобилей можно представить как марков­ский процесс, протекающий в системе (например, «поток автомо­билей—дорожные условия — средства регулирования») с дис­кретными состояниями с изменением системы в определенные состояния системы может произойти в любой момент времени t > t₀ [71].

При таком потоке для   определения вероятностей со­стояния р₁(t); p₂(t)…p_n(t) составляют систему линейных диффе­ренциальных уравнений.

При составлении уравнений пользуются графом состояния си­стемы—наглядным изображением состояния системы (рис. 111.3). На рис. 111.3 λ_ij обозначает плотность потока событий, переводя­щего систему из состояния S_i в S_j.

Для системы, показанной на рис. 111.3, дифференциальные уравнения имеют вид:

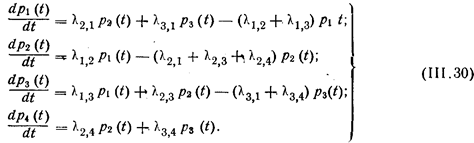
Это более реальная схема, нежели принятая Д. Дрю [24].

 Более простым случаем является марковский процесс с дис­кретными состояниями с изменением системы в определенные мо­менты 0, 1, 2, 3, ... i,... Вероятность того, что в момент t система находится в состоянии S_i обозначается p_t(t). Вероятность того что в момент (t+1) система будет находиться в состоянии S_j, равна произведениям вероятностей нахождения системы в момент t в состоянии S_i, на вероятность перехода, просуммированным по всем возможным состояниям S_i.

                                     P_j(t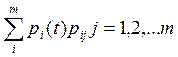+1) = ,                                                                  (III.31)

где S₁, S₂, …, S_n – состояние системы;

t₁,  t₂, …, t_n – моменты времени; p_ij – вероятность перехода x_i  → x_j.

При использовании цепей Маркова для транспортного потока могут быть рассмотрены случаи изменения состояния потока ав­томобилей при совершении какого-либо события [71]. Такими со­бытиями могут быть: догон одного автомобиля другим, обгон, маневр смены полосы, выезд нового автомобиля на дорогу. Состоя­ние всего потока может характеризоваться: числом автомобилей на данном участке дороги или условием движений автомобиля (свободные или стесненные).