Проектирование дорог для движения транспортных потоков как путь повышения эффек­тивности работы автомобильных дорог. Взаимодействие автомобилей в транспортном потоке. Макроскопические теории транспортного потока, страница 6

ΔN_t— темпы относительного прироста (см. уравнение (1.13)).

Расчеты по уравнению (1.19) несколько сложнее. Ю. М. Ситни­ковым [73] на основе преобразования уравнения (1.19) было пред­ложено уравнение, позволяющее упростить расчеты:

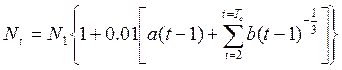,                                   (1.20)

где а  и b — эмпирические коэффициенты в уравнении (1.13); Т_c — срок служ­бы дороги.

Для прогнозирования движения во вновь ос­ваиваемых районах могут быть использованы степенные уравнения. В этих районах характерным является первоначальный рост интенсивности движения в период строительства дороги или каких-либо   промышленных объектов. После окончания строительства интенсивность движения растет медленно [5]. Для прогнозирования по такой зависимости может быть ис­пользована следующая форму­ла:

N_t=(аt³+ bt² + сt + d)^1/n    (1.21)

где а, b, с и d — эмпирические ко­эффициенты;  t- расчетный год; п —oбщее число лет прогнозирования.

Форма   логистичес­кой кривой для прогно­зирования интенсивности дви­жения установлена на основе логических   рассуждений о возможном характере измене­ния интенсивности движения по годам. Характерна тенден­ция приближения логистиче­ской кривой к некоторому уровню насыщения. Например, при прогнозировании интен­сивности  движения   таким уровнем может быть пропускная     способность    дороги (рис. 1.9).

Форма логистической кривой наиболее точно удовлетворяет дифференциаль­ному уравнению:                      

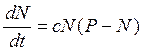,                                               (1.22)

где N — интенсивность движения; Р — пропускная способность; с — постоян­ная; t — период времени.

Решение уравнения (1.22) имеет вид

N = 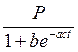.                                           (1.23)

рцс. 1.10. Пример   прогнозирования на основе

                                                                                               уравнения (1.26)

Логистическая кривая, описываемая уравнением (1.23), представляет собой S-образную кривую с асимптотами  N=0 при

t→-оо и N=Р  при t→+оо. Из уравнения (1.22) видно, что темпы роста N в процентах равны 100 с (Р—М), т. е. прямо пропорциональны разнице между N и ее асимптотой Р. Если N=Nо при t=0, то Nо(1+Ь) =P Если процент роста при t=0 известен и ра­вен 100m процентов в год, тогда

с(Р—Nо)= т,                                                                                                     (1.24)

С учетом уравнения (1.24) уравнение (1.23) примет следующий вид:

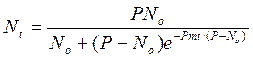                                                            (1.25)

В уравнении (1.25) отношение 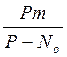характеризует скорость достижения предельного уровня, т. е. исчерпания пропускной способности. Момент времени, когда темп роста интенсивности движения начинает уменьшаться, соответству­ет точке, в которой

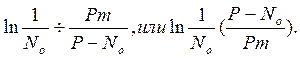
Логистическая кривая охватывает практически весь период из­менения интенсивности движения до достижения пропускной спо­собности. Поэтому ее можно применять преимущественно при долгосрочных прогнозах. При использовании этой кривой необхо­димо иметь данные о пропускной способности и данные по интен­сивности движения за последние 15 лет для определения параметров уравнения.

Логистическую кривую можно применять для прогнозирования общих показателей развития автомобильного транспорта, напри­мер числа автомобилей на душу населения как в отдельных райо­нах, так и в среднем по стране [122].

В отдельных случаях с точки зрения упрощения определения основных параметров можно использовать уравнение типа (рис. 1.10):

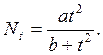                                                                                                        (1.26)

Экстраполяционные методы могут успешно применяться для краткосрочного прогнозирования. Поэтому нельзя согласиться с мнением В. Е. Кагановича и В. К. Пашкина [29, 52] о невозмож­ности применения этих методов в районах с развитой сетью дорог.