Проектирование дорог для движения транспортных потоков как путь повышения эффек­тивности работы автомобильных дорог. Взаимодействие автомобилей в транспортном потоке. Макроскопические теории транспортного потока, страница 40

1 — фактическое распределение; II — теоретическое распределение

Для этого были построены зависимо­сти R от интенсивности движения на дорогах (cм. рис. 111.6). Уста­новлено, что это распределение применимо при интенсивности в одном направлении: на двухпо-лооных дорогах до 200 авт/ч; на четырехполосных автомагистра­лях до 500 авт/ч, на шестиполос­ных    автомагистралях     до 1100 авт/ч. Отмечено, что преде­лы применимости распределения Пуассона резко меняются в раз­личных условиях  (рис. 111.8).

Учитывая, что применимость распределения Пуассона огра­ничена, различными  авторами [23, 58, 104, 111] предлагались поправки к этому распределе­нию, позволяющие   расширить область его применимости (рис. 111.9). Интерес к этому распре­делению объясняется тем, что оно позволяет упростить анали­тические решения задач движе­ния потока автомобилей в раз­ных дорожных условиях. Были предложены поправки:

введение коэффициента в эк­споненту

          p_∆t = e^-μλ  ;               (111.34)

добавление функции, учиты­вающей условия движения (фун­кции влияния)

                                                        p_∆t = e^-λ + Δp_λ,                                                                           (111.35)

где  Δp₂— функция влияния;

введение коэффициента, получаемого из наблюдений;

учет невозможности существования интервала менее Δt_min (смещенное распределение).

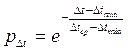                                                                    .                                                                (III.36)

Однако введение различных поправок не позволяет добиться существенного расширения диа­пазона применимости распределе­ния Пуассона. Так, введение ко­эффициента в экспоненту и ис­пользование смещенного распре­деления позволяет повысить верх­нюю границу применимости на двухполосных    дорогах    до 250 авт/ч.

Применимость логарифмиче­ски нормального распределения. Этот закон распределения может быть использован для описания интервалов и дистанций внутри пачек или групп автомобилей ли­бо при колонном движении, т.е.

при интервалах, на которых автомобили взаимодействуют между собой (рис. 111.10).

Применимость смешанных распределений. С целью получе­ния более широкого диапазона применения различными автора­ми использовались смешанные распределения. Несомненно, что смешанные распределения позволяют более детально учитывать состав движения, состояние потока автомобилей, выделяя наибо­лее характерные группы автомобилей.

Из смешанных распределений следует отметить следующие:

двухкомпонентные уравнения смеси и распределение Шуля

p_Δt = 0.7 (111.37)

распределение Ондермарка

                                           p(Δt) = 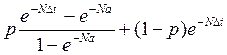 ;                                                                    (111.38)

  трехкомпонентное уравнение смеси (предложенное Е. М. Лобано­вым)

 p(Δt) = A ;                                                                   (111.39)

многокомпонентное уравнение смеси (предложенное В.В. Сильяновым)

p_Δt =p₁λ,                                                     (111.40)

где а — коэффициент влияния; N — интенсивность движения; А, В, С — коэффициенты, учитывающие количество свободных, частично связанных и связанных автомобилей в потоке, — вероятности появления интервалов определенной длины в свободной и частично связанной части потока автомобилей;  p₁, p₂, …, p_к — количество автомобилей разных скоростных групп, зависящее от дорожных условий, %.