|
Рис. 111.3. Граф состояния системы |
|
Рис. 111.4. Граф состояния потока автомобилей |
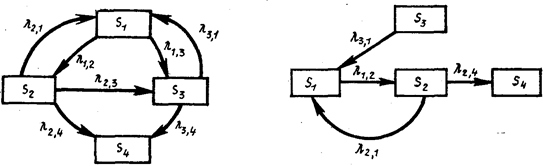
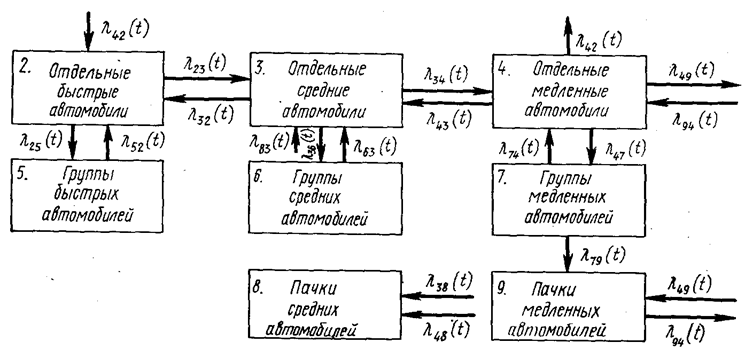
Рис. 111.5. Граф возможных состояний транспортного потока при введении запрета обгонов и ограничения скорости движения
Рассмотрим возможный граф состояния потока автомобилей на участке дороги определенного протяжения (рис. 111.4). Выделим, например, следующие состояния: Sо—начальное состояние потока; S1 — какой-либо автомобиль догнал впереди идущий; S2— произошел обгон; Sз — выехал новый автомобиль на данный участок; S4 — автомобиль покинул данный участок.
Для этого потока можно определить вероятности: совершения обгона в пределах рассматриваемого участка дороги, вероятности догона быстро движущимся автомобилем медленно движущегося и т. п.
В п. V.5 рассмотрено статистическое моделирование транспортного потока по принципу особых состояний, основанных на цепях Маркова. Цепи Маркова могут быть также использованы для оценки состояния потока автомобилей при выезде на основную дорогу или загрузке стоянки автомобилями. В этом случае состояние системы определяется числом автомобилей в очереди или на стоянке.
На рис. 111.5 показан граф возможных состояний транспортного потока, вероятность существования которых определяется по. дифференциальным уравнениям (111.32), полученным Н. Н. Чуклиновым и М.Т. Работягой.
Понятие цепей Маркова было использовано В. В. Филипповым для изучения характеристик движения потока автомобилей, в частности для оценки вероятности движения быстро движущегося автомобиля в свободном режиме [84].
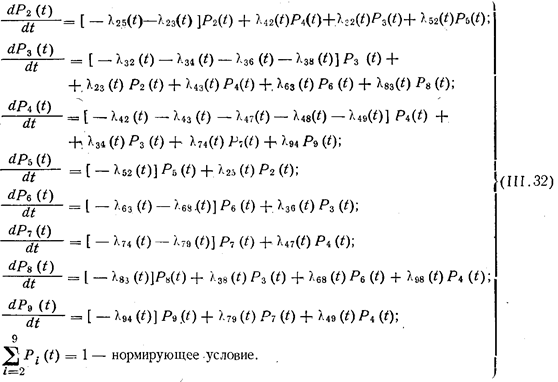
III. ОЦЕНКА ПРИМЕНИМОСТИ РАЗЛИЧНЫХ МОДЕЛЕЙ РАСПРЕДЕЛЕНИЯ ИНТЕРВАЛОВ В ТРАНСПОРТНОМ ПОТОКЕ
Важным показателем движения потока автомобилей низкой плотности является распределение интервалов между движущимися друг за другом автомобилями. Это распределение служит основой расчета всех характеристик взаимодействия автомобилей в потоке автомобилей низкой плотности. От того, насколько надежны теоретические результаты интервалов, зависит и надежность оценки всех характеристик потока.
Были определены области практической применимости следующих закономерностей: экспоненциальных распределений, распределения смеси, распределения Пирсона III типа, логарифмически нормального распределения. Нормальные кривые распределения и смеси этих кривых наиболее надежно описывают распределение значений скоростей движения [23], поэтому в данном параграфе они не рассмотрены. Д. Дрю предложил также использовать для описания распределения скоростей распределение Пирсона I типа [24]. Видимо, эта кривая лучше описывает распределение скоростей при значительном смещении моды кривой распределения вправо (или влево), т. ё. при преобладании в потоке какой то скоростной группы автомобилей.
|
|
|
Рис. 111.6. Применимость распределения Пуассона: 1— четырехполосная автомагистраль; 2— шестиполосная автомагистраль |
Критерий проверки надежности распределения. Наиболее
нагляден критерий В. И. Романовского,
основанный на применении критерия согласия ![]() [62]:
[62]:
R
= 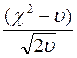 ,
(111.33)
,
(111.33)
где ν — число степеней свободы.
При R ≥ 3 расхождение считается существенным, при R<.3— случайным.
Применимость экспоненциальных распределений. Наиболее характерным и простейшим представителем этого класса распределений является распределение Пуассона [уравнение (111.5)]. Была оценена возможность применения этого распределения на горизонтальных прямых участках различных типов дорог: на двухполосных дорогах и на автомагистралях с четырьмя и шестью полосами движения (рис. 111.6,111.7).
|
|
|
|
Рис. 111.7. Распределение интервалов во времени на многополосных автомагистралях с осреднением по кривой распределения Пуассона (по данным А. Н.. Красникова):
а — четырехполосная автомагистраль; б — шестиполосная автомагистраль;
1 - N =400 авт/ч (R =1,8); 2 — N = 1160 авт/ч (R =9,4); 3 - N= 1020 авт/ч (R = 1,45); 4 -N = 2090 авт/ч (R= 8,3);
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.