математическая статистика — при планировании экспериментов, анализе аварийности, обработке результатов экспериментов;
теория массового обслуживания — при решении задач, связанных с движением потоков низкой и средней интенсивности, для решения технико-экономических задач по выбору размеров элементов дороги, для оценки влияния средств регулирования на движение потока автомобилей;
теория игр— при анализе аварийных ситуаций на дороге, вариантной оценке проектных решений;
методы математического программирования (линейное, динамическое, нелинейное) — при оценке пропускной способности сети дорог и отдельных элементов дорог, при изучении распределения, движения по сети дорог, прогнозировании интенсивности движения и др.;
теория сервомеханизмов — при решении задач управления автомобилем, задачи следования за лидером и др.;
моделирование — при решении всех задач проектирования дорог и выбора средств управления движением, являющимся универсальным методом изучения движения потоков автомобилей;
теория графов — при проектировании сети дорог [88], при исследовании распределения движения по сети дорог и др.;
теория обучения — при решении проблемы управления движением.
Решение задач, связанных с определением характеристик движения потоков автомобилей в различных дорожных условиях при наличии средств управления движением, требует учета качественного состояния потока. На дорогах может быть четыре состояния потока автомобилей (см. п. 11.2), что необходимо учитывать при выборе математического аппарата и разработке моделей движения потока автомобилей.
При низкой плотности потока автомобилей появление автомобиля в данном створе или на участке дороги является случайным событием. Поэтому для изучения движения потоков автомобилей низкой . плотности может быть использован аппарат теории вероятностей, изучающей закономерности в случайных явлениях. В теоретическом описании движения транспортных потоков низкой и средней плотности основное место занимает теория массового обслуживания, позволяющая определить такие характеристики потока, как размер групп автомобилей, потери времени и т.п. Теория случайных функций может быть применена для изучения отдельных характеристик-движения и взаимодействия автомобилей, а также действий водителей. Учитывая, что транспортный поток представляет собой сложную систему при решении задач, связанных с переходом потока автомобилей из одного состояния в другое, могут применяться цепи Маркова.
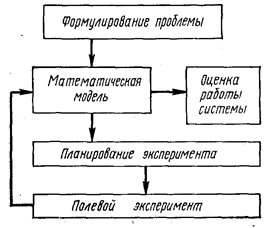
Рис. 111.1. Этапы разработки математической модели сложной системы
По мере увеличения плотности потока автомобилей возникает необходимость применять и другие математические аппараты. Для описания плотных потоков автомобилей необходимо использовать математический аппарат, описывающий движение сплошной среды или аппарат, позволяющий наиболее эффективно описать взаимодействие между автомобилями в потоке с учетом наличия человека в качестве оператора.
Исходя из этого можно выделить две большие группы теорий транспортных потоков: стохастические (вероятностные) теории и динамические теории. При разработке моделей движения потоков автомобилей необходимо учитывать принципы и этапы разработки сложных систем (рис. 111.1), основными из которых являются анализ принятой модели, критическая ее оценка и оценка соответствия модели, результатам натурных экспериментов.
III. 2. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ В ТЕОРИИ ТРАНСПОРТНЫХ ПОТОКОВ
Наиболее важной характеристикой движения транспортного потока является распределение интервалов между движущимися Друг за другом автомобилями.
В теории вероятностей распределение интервалов между случайными событиями является основой для вывода расчетных формул при определении характеристик случайного процесса.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.