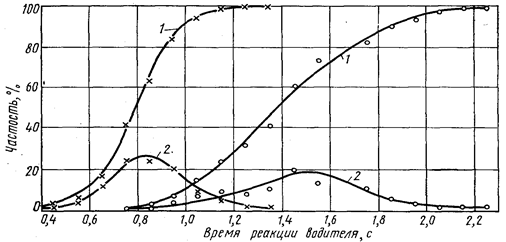
Рис. 1У.5. Распределение значений времени реакции водителя (по данным измерений в ходовой лаборатории, проведенных Е. М. Лобановым):
Х — двухполосная дорога при ожидаемом сигнале; О— двухполосная дорога при неожиданном сигнале; 1 — кумулятивная кривая: 2 — кривая распределения
С учетом перечисленных выше уточнений основное уравнение упрощенной динамической теории может быть представлено в следующем виде:
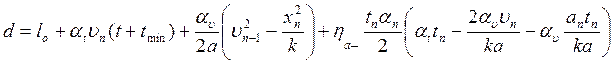(IV.4)
где d— расстояние между автомобилями; d = xn-1 – xn – ln-1; ln-1— длина (п-1)-го автомобиля; lo — расстояние между остановившимися автомобилями; νn — скорость автомобиля, движущегося сзади; а — максимальное ускорение, которое может ожидать водитель n-го автомобиля; tmin — минимальное время, необходимое водителю для осознания ситуации; tn — продолжительность реакции водителя n-го автомобиля; k— показатель, учитываемый в случае, если водитель n-го автомобиля использует ускорение менее максимального (k ≤ 1,0); ηa - коэффициент, зависящий от способности водителя n-го автомобиля чувствовать влияние принимаемого ускорения; αt — показатель безопасности (α > 1), зависящий от величины времени запаздывания; αv — показатель безопасности, зависящий от разности скоростей [137].
αv ≥
1 при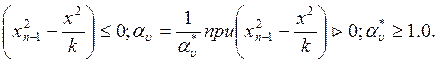 
Расстояние между остановившимися автомобилями принимается в зависимости от скорости движения:
v, км/ч ...................... 20 40 60 80 100
lo, м....................... 3 6 10 12 15
Расстояние, вычисленное по уравнению (IV.4), состоит из следующих составляющих: минимального расстояния между остановившимися автомобилями; расстояния, проходимого за время запаздывания; расстояния, принимаемого в зависимости от разности скоростей (третье слагаемое уравнения); поправки на влияние величины ускорения, принимаемого водителем (четвертое слагаемое уравнение). Учет особенностей торможения, несомненно, позволяет получать более точные значения расстояний.
Особенностью применения упрощенных динамических моделей является распространение на весь поток значений расстояний, подученных для двух автомобилей. Этот принцип не совсем правилен, так как не учитывается разнородный состав движения. Поэтому целесообразна следующая последовательность расчетов на основе уравнений упрощенных динамических теорий: расчет по уравнениям (1У.З) или (1У.4) для всех сочетаний автомобилей; расчет на основе эмпирической зависимости для тех же сочетании автомобилей; определение средних значений по теоретической и эмпирической зависимостям; принятие меньшего значения.
IV. 3. ДИНАМИЧЕСКАЯ ТЕОРИЯ СЛЕДОВАНИЯ ЗА ЛИДЕРОМ
При решении вопросов, связанных с уменьшением числа дорожно-транспортных происшествий (особенно вызванных столкновением автомобилей между собой), необходимо детально изучить взаимодействие движущихся друг за другом автомобилей.
Теория «следования за лидером» является развитием теории упрощенных динамических моделей, она основана на гипотезе о существовании определенной закономерности взаимодействия автомобилей, движущихся друг за другом на близком расстоянии. Дифференциальное уравнение теории «следования за лидером» получено из начального условия, что все автомобили движутся в колонне на расстоянии, требуемом правилами дорожного движения [105]. Из рис. IV.6 видно, что при соблюдении требований правил движения координаты положения п-го и (n+1)-го автомобилей можно выразить зависимостью:
Xn+1 = xn + (lo + tpvn)
+ln+1,
(IV.5)
где lо — минимальное расстояние между стоящими автомобилями; lр vn — расстояние между автомобилями, устанавливаемые в зависимости от скорости движения; ln+1 — длина автомобиля; п — порядковый номер автомобиля.
Рис. 1У.6. Координаты положения автомобилей при движении в колонне
Дифференцируя уравнение (1У.5) по времени, получаем
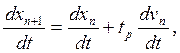(IV.6)
Уравнение (1У.6) может быть выражено через скорость в следующем виде:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.