Проектирование дорог для движения транспортных потоков как путь повышения эффек­тивности работы автомобильных дорог. Взаимодействие автомобилей в транспортном потоке. Макроскопические теории транспортного потока, страница 2

Последовательность расчета характеристик случайной функции скорости по известным характеристикам случайной функции продольного профиля следую­щая [17]:

определяют математическое ожидание скорости движения

m_v(t)=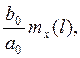                                                                         (1.3)

где а₀,и 6₀—переводные коэффициенты;

по корреляционной функции р(τ) определяют спектральную плотность про­дольного профиля

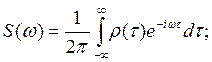                                                                    (1.4)

определяют квадрат модуля частотной характеристики

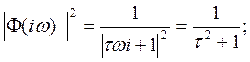                                                               (1.5)

определяют спектральную плотность скорости движения

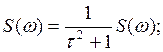                                                                        (1.6)

по спектральной плотности S_v(ω) определяют корреляционную функцию скорости

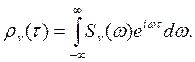                                                               (1.7)

Эта методика позволяет получить средние показатели условий движения на маршрутах большого протяжения.

По величине математического ожидания скорости и корреля­ционной функции скорости можно оценивать необходимость при­менения средств организации движения, позволяющих уменьшить величину колебания значений скорости. Такой же анализ случай­ных изменений с позиции теории случайных функций можно сде­лать для таких характеристик, как траектории движения, ускоре­ние и др.

При движении автомобиля по горизонтальному участку (т. е. при отсутствии влияния продольного профиля) наблюдается лишь «шум» скорости, т. е. небольшие колебания величин скоростей дви­жения, вызванные действиями водителей, случайным влиянием сил сопротивления движению и т. п. При наличии продольных уклонов и кривых в плане появляются резкие изменения функции скорости, которые носят постоянный характер и наблюдаются у всех авто­мобилей.

При этом сохраняется и «шум» скорости около ее средней ве­личины, зависящей от геометрических элементов дороги.

Из приведенного выше описания методики определения пара­метров случайной функции видно, что влияние на эти параметры геометрических элементов дороги наиболее существенно по срав­нению с влиянием других случайных факторов. При движении по­тока автомобилей будем иметь семейство случайных функций для отдельных автомобилей.

Для более детального выяснения характера изменения случай­ной функции скоростей движения вдоль дороги как показателя безопасности движения представляется интересным изучить спект­ральный состав функции скорости. При этом критерием будет слу­жить дисперсия этой функции.

Такое разложение может быть выполнено на основе преобразо­вания Фурье [17]. Практически любая функция может быть заме­нена серией синусоид.

Можно выделить следующие группы случайных факторов, воз­действующих на автомобиль: наличие на дорогах различных води­телей (вызывает «шум» скорости); различие технического состоя­ния и динамических качеств автомобилей (вызывает «шум» скоро­сти и ускорения); изменение климатических условий (вызывает изменение скорости); изменение дорожных условий (постоянный «фон», накладывающийся на «шум» скорости).

Кроме этих факторов, значительное влияние на скорость ока­зывает наличие на дороге средств организации движения. По дли-де дороги эти средства располагаются случайно.

Каждый водитель, проезжающий по дороге, воспринимая слу­чайный поток информации, изменяет режим движения автомоби­ля. Такой поток можно рассматривать как простейший, подчиня­ющийся закону Пуассона.

-, Случайный характер изменения элементов дороги и характе­ристик движения потоков автомобилей указывает на возможность использования теории случайных функций, при этом широкое при­менение может найти развивающаяся теория нестационарных случайных процессов.

I. 2.ЗАКОНОМЕРНОСТИ ИЗМЕНЕНИЯ ИНТЕНСИВНОСТИ ДВИЖЕНИЯ НА АВТОМОБИЛЬНЫХ ДОРОГАХ

Важнейшей характеристикой транспортного потока является интенсивность движения, величиной которой определяются значи­мость дороги, геометрические элементы, требуемый уровень орга­низации движения, финансирование службы эксплуатации доро­ги и т. п. Величина интенсивности движения используется на всех этапах проектирования дорог и при выборе средств и методов ор­ганизации движения. Интенсивность движения меняется случай­но как во времени, так и в пространстве (по длине и ширине до­роги).