Курс практических занятий по теме «Циклические коды» дисциплины «Передача дискретных сообщений», страница 37

2⁷- 1= 127                            2²³-1= 47×178481

2⁸- 1= 3×5×17                      2²⁴-1= 3×3×5×7×13×17×241

2⁹- 1= 7×73                           2²⁵-1= 31×601×1801

2¹⁰-1= 3×11×31                     2²⁶-1= 3×2731×8191

2¹¹-1= 23×89                         2²⁷-1= 7×73×262657

2¹²-1= 3×3×5×7×13               2²⁸-1= 3×5×29×43×113×127

2¹³-1= 8191                            2²⁹-1= 233×1103×2089

2¹⁴-1= 3×43×127                    2³⁰-1= 3×3×7×11×31×151×331

2¹⁵-1= 7×31×151                    2³¹-1= 2147483647

2¹⁶-1= 3×5×17×257                2³²-1= 3×5×17×257×65537

2¹⁷-1= 131071                         2³³-1= 7×23×89×599479

2¹⁸-1= 3×3×3×7×19×73          2³⁴-1= 3×43691×131071

2.5. Алгоритм разложения Хⁿ+1 на неприводимые сомножители.

Обобщением вышеизложенного в отношении разложения двучлена вида  Хⁿ+1

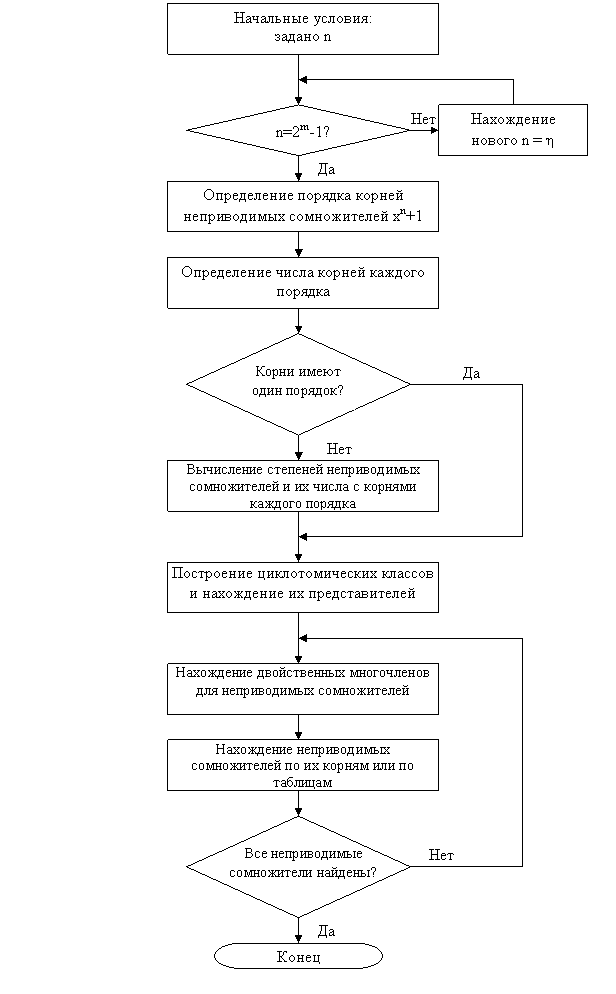
на неприводимые над двоичным полем сомножители представлено в виде приведенного в данном разделе алгоритма. Проиллюстрируем применение данного алгоритма двумя примерами.

Пример 2.5.1.  Разложить Х²¹+1 на неприводимые сомножители над GF(2).

                          Решение

Шаг 1. Задано значение степени двучлена n =21.

Шаг 2. Заданное значение n =21 не может быть представлено в виде n =2– 1.

Шаг 3. Из табл.2.4.2. находим ближайшее к 21 число, которое делится на 21 и может быть представлено в виде 2– 1. Таким числом является  63, т.е. η = 63 и  m = 6.

Шаг 4. Неприводимые сомножители Х²¹+1 были рассмотрены в Примере 2.4.1. Как они были определены ? Число 21=3×7. Это означает, что в разложение Х²¹+1 входят неприводимые сомножители двучленов Х³+1  и  Х⁷+1. Порядок их корней равен  3 и 7 соответственно. Кроме того, Х²¹+1, безусловно, имеет корни порядка 21.