Элементы полей GF(26),GF(24),GF(23),GF(22) и GF(2) входят в состав GF(212). При этом β = α65 , т.к. β63 = α4095 = 1 = (α65)63 . Аналогично γ = α273 ,δ = α585 , ε = α1365 , ζ = α4095 . Связь между рассмотренными полями иллюстрирует рис.1.1.
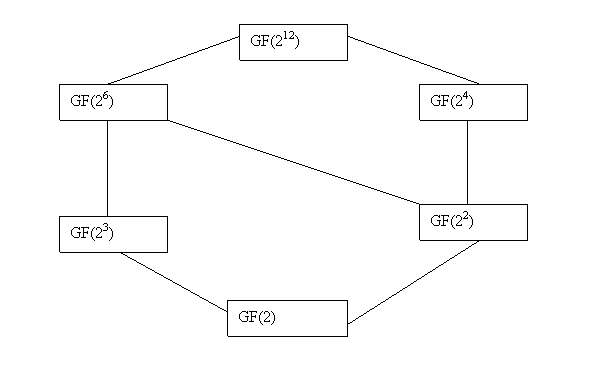
Рис.1.1.Поле GF(212)и его подполя
Глава.2.Многочлен Хn-1, его корни и неприводимые сомножители.
2.1.Связь между корнями Хn-1 и элементами поля GF(q).
Многочлен Хn-1, его неприводимые сомножители и их корни играют существенную роль в построении важнейшего класса групповых кодов-циклических кодов. Знание корней сомножителей Хn-1 позволяет решить задачу выбора требуемого кода для конкретного дискретного канала.
Рассмотрим общий случай:
Пусть Хn-1 задан над полем GF(q). Известно, что GF(q) имеет циклическую группу из q-1 своих ненулевых элементов.
Порядок каждого ненулевого элемента GF(q) не может быть выше q-1, а это означает, что αq-1=1 для любого ненулевого элемента α из GF(q),т.е. любой ненулевой элемент GF(q) обращает Хq-1-1 в нуль, а, значит, является его корнем. Поскольку Хq-1-1 имеет ровно q-1 корней, то, следовательно, все ненулевые элементы GF(q) являются корнями Хq-1-1.
Таким образом,
|
имеется однозначное соответствие между корнями Хq-1-1 и ненулевыми элементами GF(q). |
В случае двоичных циклических кодов нас интересуют многочлены с корнями из расширенных полей Галуа GF(2m). В соответствии с полученным выше результатом справедливо утверждение:
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.