Промышленность \ Добыча, хранение и транспортировка нефти и газа

Методы повышения эффективности процессов добычи и транспорта газа, страница 4

l

2

3

4

5

8

"] 10

.     Х{

-0,1

-r-0,4

^0,9

+0,5

0,0

1,4

0,3 1

0,4

~1,4

^1,2:

i

11

12

IS

.14

15

J6

17

181

19

20

-1,1

-1,1

-1,1

-0,9 j

-^0,8

-6?8

—0,7

-0,7

-4),6

-4),S

/

21

22

23

24

25

26

-"27. ■■

U9

30 Л

xt

-0,6

—0,6

—0,5

.—0,4

-0,1

-4),1

-0,1

0-1

0,2

0,4

i

31

32

33

34

55

36    ь

37

38

39

40

xt

1,1

1,1

1,6

0,8

1,9

1Д

1,9

2,0

2,1

0,7

.   ■    : ■

- ё

41

42

43

44

45

46

47

48

49

50

Xi

-0,4

-0,1

1,3

1,0

0,4

1,4

0,7

0,8

0,0

1,0

i

51

52

53

54

55

56

57

58

59

60

Xi

0,2

-0,4

—0,3

0,3

0,4

0,1

0,6

2,0

0,4

0,1'

i

61

62

63

64

65

66

67

68

69

70

Xi

—0,3

—0,0

-1,9

-4,2

-1,0

-1,0

—0,7

—Q,7

—0,6

—0,5

i

71

72

73

74

75

76

77

1  78

Xi

-0,3

-0,2

-4,1

0,0

0.5

1,0

—1,1

-0,6]

Пример 1.1. Обозначим случайную величину ГН через У. Подвергнем У функциональному преобразованию:

yt—i— реализация У (i=l, 2, ..., 78);

.     78

В результате получены реализации xi(t = l, 2, ..., 78) пре­образованной случайной величины х, которые представлены в табл. 1.2.

Задача состоит в проверке гипотезы о том, что случайная величина х подчинена стандартному нормальному закону с «функцией распределения

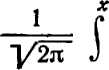
—по

После расположения Х{ в возрастающем порядке статистика -Л(о2 оказалась равной 0,0878, что обеспечивает неравенство лш2<(то2)кр вплоть до значений у—0,5. Следовательно, на уровне значимости 0,5 гипотеза о нормальности х принимается.

АССОЦИАТИВНЫЙ АНАЛИЗ

При статистической обработке экспериментальных материалов в пер'вую очередь необходимо установить, существует ли связь между двумя или несколькими факторами, разбитыми на груп­пы по качественным или количественным признакам.

В таких случаях экспериментальные данные разбиваются на группы, каждая из которых определяет некоторые количе­ственные или качественные признаки совокупности данных.

С помощью ассоциативного анализа [4] можно предвари­тельно оценить, влияет ли на рассматриваемый показатель про­цесса тот или иной фактор и есть ли смысл проводить более подробные исследования, например дисперсионный и корреля­ционный анализы.

Мера связи двух качественных признаков, состоящих из двух групп, определяется коэффициентом ассоциации. Мера •связи для качественных признаков» каждый из которых состоит «более чем из двух групп, определяется коэффициентом взаим­ной сопряженности [9].

Рассмотрим применение ассоциативного анализа на конкрет­ных примерах.

10


Скачать файл