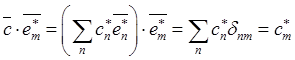 ,
, ![]() .
.
Через физические компоненты представим и квадрат модуля вектора
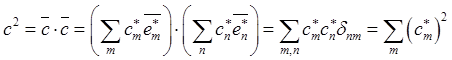 .
.
Следовательно, модуль вектора и его направление относительно элементов базиса в точке приложения вектора определяются формулами
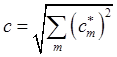 ,
, 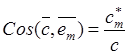 .
(7.12)
.
(7.12)
8. Представление движения точки в ортогональной системе.
Установим уравнения движения точки в ортогональной криволинейной системе координат и на их основе укажем способы вычисления ее скорости и ускорения.
1°. Уравнения движения точки.
В декартовых
координатах уравнения движения точки имели вид ![]() .
Поскольку криволинейные координаты являются функциями декартовых, то они также
будут изменяться со временем
.
Поскольку криволинейные координаты являются функциями декартовых, то они также
будут изменяться со временем
![]()
![]() .
(8.1)
.
(8.1)
Эти функции и называют уравнениями движения точки в криволинейных координатах. Эти равенства дают также параметрические уравнения траектории точки.
Основываясь на
допущениях относительно функций ![]() и
и ![]() найдем, что сложные функции (8.1)
найдем, что сложные функции (8.1) ![]() . Производные
. Производные ![]() и
и ![]() называют соответственно
называют соответственно ![]() криволинейными скоростями и криволинейными
ускорениями. Ниже будет показано, что через них можно выразить обычные скорость
и ускорение.
криволинейными скоростями и криволинейными
ускорениями. Ниже будет показано, что через них можно выразить обычные скорость
и ускорение.
2°. Вычисление скорости точки.
При
рассмотрении движения точки в криволинейных координатах вектор-радиус зависит
от времени через посредство этих координат ![]() .Поэтому
согласно определению скорости будем иметь выражение
.Поэтому
согласно определению скорости будем иметь выражение
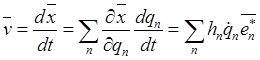 .
(8.2)
.
(8.2)
Вектор скорости может быть
представлен также через свои физические компоненты в виде ![]() . Из этих двух представлений в силу
единственности следует, что физические компоненты скорости определяются в виде
. Из этих двух представлений в силу
единственности следует, что физические компоненты скорости определяются в виде
![]()
![]() .
(8.3)
.
(8.3)
То есть физические компоненты скорости пропорциональны соответствующим криволинейным скоростям, причем коэффициентами пропорциональности служат коэффициенты Ламе.
Модуль вектора скорости и его направление относительно элементов базиса определяются формулами вида (7.12):
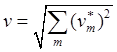 ,
, 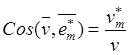 .
(8.4)
.
(8.4)
3°. Определение движения точки по скорости и начальному положению.
Пусть известны
физические компоненты скорости точки как непрерывно-дифференцируемые функции
времени ![]() и ее начальное положение, задаваемое ее
координатами в начальный момент
и ее начальное положение, задаваемое ее
координатами в начальный момент ![]() :
: ![]() . Тогда в силу формул (8.3) имеем начальную
задачу для нормальной системы трех дифференциальных уравнений первого порядка
. Тогда в силу формул (8.3) имеем начальную
задачу для нормальной системы трех дифференциальных уравнений первого порядка
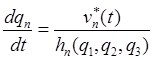 ,
, ![]()
![]() (8.5)
(8.5)
для
определения трех функций времени ![]() (В задаче (8.5)
коэффициенты Ламе полагаются заданными).
(В задаче (8.5)
коэффициенты Ламе полагаются заданными).
Допущения о
функциях ![]() и
и ![]() обеспечивают
существование и единственность решения этой задачи. Тем самым скоростью и
начальным положением уравнения движения точки однозначно определяются как
решение задачи (8.5).
обеспечивают
существование и единственность решения этой задачи. Тем самым скоростью и
начальным положением уравнения движения точки однозначно определяются как
решение задачи (8.5).
4°. Вычисление ускорения точки.
Вектор ускорения точки в криволинейной системе координат представляется разложением
![]() .
(8.6)
.
(8.6)
Установим выражения для его физических компонент. Используя известные представления для компонент, ускорения и элементов базиса, будем иметь
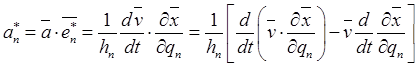 .
(8.7)
.
(8.7)
Покажем, что выражение в квадратных скобках представимо через квадрат скорости. Вектор скорости точки является функцией криволинейных координат и скоростей
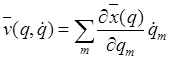 . (8.8)
. (8.8)
Рассматривая криволинейные
координаты и скорости ![]() ,
, ![]() в
качестве независимых переменных, продифференцируем (8.8) по скорости
в
качестве независимых переменных, продифференцируем (8.8) по скорости ![]()
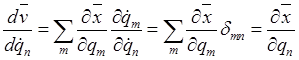 . (8.9)
. (8.9)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.