Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 47

при этом скорость и ускорение точки не могут быть произвольными величинами, а должны удовлетворять некоторым ограничениям. Установим вид этих ограничений.

Дифференцируя по времени равенство (27.2), получим ограничение на скорость:

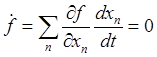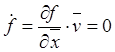   или   .                                                                        (27.3)

Вектор, декартовыми компонентами которого служат частные производные от функции  по координатам, называют градиентом этой функции и обозначается через

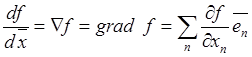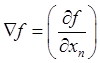   (или ).                                                       (27.4)

Как показывается в геометрии  направлен по нормали к поверхности  в сторону возрастания функции .

Условие (27.3) означает, что скорость ортогональна градиенту поверхности, следовательно, она принадлежит касательной плоскости поверхности. Представив градиент (27.4) в виде ,  – орт нормали к поверхности, условие (27.3) можно записать в виде

    , т.е. связь ограничивает только нормальную к поверхности составляющую скорости, касательная же составляющая скорости может быть произвольной.

Дифференцируя по времени равенство (27.3), получим ограничение на ускорение

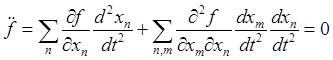 или ,                     (27.5)

где двойной градиент функции определяется матрицей ее вторых производных

.

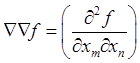Выражая градиент функции в виде , устанавливаем, что ограничению на ускорение (27.5) можно придать вид

,   , т.е. как и в отношении скорости, связь ограничивает значение только нормальной к поверхности составляющей ускорения, касательная же к поверхности составляющая ускорения остается произвольной.

3°. Основной закон динамики при движении по поверхности.

Пусть точка  массы  движется по поверхности  под действием силы . Закон движения свободной точки  не применим к этому случаю, так как определенное из него ускорение в общем случае удовлетворяют ограничению на ускорение (27.5):

.

При движении по поверхности основной закон обобщается в виде

,                                                                                                                       (27.6)

т.е. принимается, что на точку, кроме силы , действует еще некоторая сила , обусловленная присутствием связи и называемая реакцией связи. Реакция  должна быть такой, чтобы найденное из (27.6) ускорение уже удовлетворяло ограничению (27.5).

Закон (27.6) при этом имеет тот же вид, что и закон движения свободной точки, когда к действующей силе присоединена и реакция связи:

“Несвободную точку можно рассматривать как свободную, если отбросить связь и заменить ее действие силой – реакцией связи”.

Установим общий вид реакции связи. Представим реакцию в виде двух составляющих, одна из которых параллельна градиенту поверхности, а другая ортогональна ему (Рис.63):

,   ,   .                                                                                (27.7)

Силу  называют нормальной реакцией (силой давления),  – множителем связи, а  – тангенциальной реакцией (силой трения). Подстановка ускорения, определенного из закона (27.6) (записанного с учетом (27.7)):

,                                              (27.8)

в ограничение (27.5) приводит к равенству

,

которое (ввиду ) определяет множитель связи

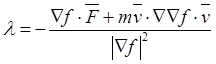.                                  (27.9)

Таким образом, уравнение связи определяет реакцию связи не полностью, а только ее нормальную составляющую. Для установления вида тангенциальной реакции требуется использовать другие соображения. На основе экспериментального исследования движения тела по поверхности было установлено, что сила трения пропорциональна модулю давления и направлена против движения

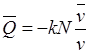,   .                                                                                                 (27.10)

Это утверждение называют законом Кулона, а множитель  – коэффициентом трения (его находят экспериментально).

Заметим, что при равновесии точки на поверхности (когда направление силы трения не определено) закон Кулона записывают для модуля силы трения: , где коэффициент  как показывают эксперименты несколько больше, чем .