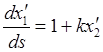 ,
, 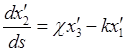 ,
, 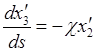
и с помощью обозначений (23.8) представим в форме
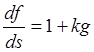 ,
, 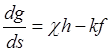 ,
, 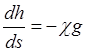 .
(23.11)
.
(23.11)
Система естественных уравнений (23.9)
и дополнительных уравнений (23.10), (23.11) уже замкнута (семь ее уравнений
служат для определения семи функций дуги: ![]() ) и
определяет естественную модель “точечное тело”.
) и
определяет естественную модель “точечное тело”.
Эта модель содержит как конечные, так и дифференциальные уравнения. Конечные уравнения, вообще говоря, позволяют выразить кривизну и кручение через другие величины и тем самым сократить число искомых функций.
Действительно,
вместо уравнения ![]() в (23.9) можно взять
эквивалентные ему равенства
в (23.9) можно взять
эквивалентные ему равенства
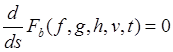 ,
, ![]() .
(23.12)
.
(23.12)
Первое из них после выполнения дифференцирования и замены в полученном результате производных их значениями из уравнений модели приводит к конечному уравнению
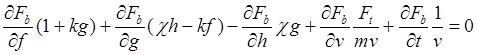 .
(23.13)
.
(23.13)
Полагая, что на рассматриваемом интервале дуги движение происходит без остановок и что кручение фактически входит в (23.13):
![]() ,
, 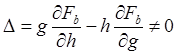 , найдем, что конечные уравнения
модели определяют кривизну и кручение
, найдем, что конечные уравнения
модели определяют кривизну и кручение
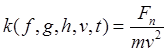 ,
,
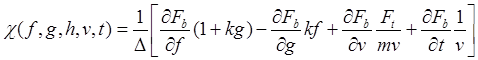 .
(23.14)
.
(23.14)
Что касается дифференциальных уравнений, то в силу (23.14) они образуют замкнутую систему пятого порядка
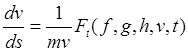 ,
, 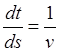 ,
, 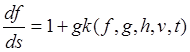 ,
,
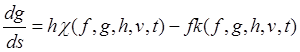 ,
, 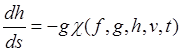 .
(23.15)
.
(23.15)
Так как правые части (23.15) не содержат аргумента – дуги, то порядок этой системы можно понизить на единицу. Путем преобразования уравнений системы с помощью второго из них, получаем систему четвертого порядка
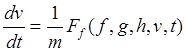 ,
, 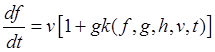 ,
,
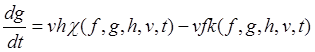 ,
, 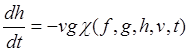 .
(23.16)
.
(23.16)
Интегрирование этой системы при начальных условиях
![]()
определяет функции ![]() , а согласно (23.14) – и
, а согласно (23.14) – и ![]() . Зависимость дуги от времени определяется
квадратурой
. Зависимость дуги от времени определяется
квадратурой
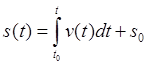 .
(23.17)
.
(23.17)
Таким образом, порядок естественной дифференциальной системы (23.16) на две единицы ниже порядка координатной системы, что делает ее привлекательной при решении ряда задач.
4°. Основные задачи динамики точки.
Дифференциальные уравнения движения позволяют решать две основные задачи динамики: прямую и обратную. В прямой задаче по известным кинематическим уравнениям движения точки определяется действующая на нее сила. В обратной задаче по известным компонентам силы и начальному состоянию движения точки определяются ее кинематические уравнения движения.
Прямая и обратная задачи не равнозначны по трудности. Если первая из них решается сравнительно легко, то вторая – весьма трудна, и аналитическое решение ее в общем случае неизвестно; его можно найти при частных видах сил. В общем случае решение находят приближенно при помощи численного счета с использованием ЭВМ.
Рассмотрим эти задачи подробнее.
24. Определение силы по движению.
1°. Определение силы в зависимости от времени.
Рассмотрим
подробнее прямую задачу динамики. Будем считать, что для точки ![]() массы
массы ![]() задано
движение в декартовой инерциальной системе координат с помощью уравнений
задано
движение в декартовой инерциальной системе координат с помощью уравнений
![]()
![]() .
(24.1)
.
(24.1)
Полагаем, что ![]() – дважды непрерывно дифференцируемые
функции
– дважды непрерывно дифференцируемые
функции ![]() . Покажем, что этих данных достаточно для
нахождения силы.
. Покажем, что этих данных достаточно для
нахождения силы.
По уравнениям
(24.1) находим компоненты скорости и ускорения: ![]() .
Обращаясь, далее, к дифференциальным уравнениям движения точки в декартовых
координатах
.
Обращаясь, далее, к дифференциальным уравнениям движения точки в декартовых
координатах ![]() и используя полученные выражения
ускорений, найдем, что компоненты силы определяются как функции времени
выражениями
и используя полученные выражения
ускорений, найдем, что компоненты силы определяются как функции времени
выражениями
![]()
![]() .
(24.2)
.
(24.2)
Найденные компоненты определяют вектор силы в декартовом базисе согласно формуле
![]() .
(24.3)
.
(24.3)
Таким образом, по массе и уравнениям движения действующая сила однозначно определяется в каждый момент времени.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.