Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 15

Соответственно этому будут параллельны и линии узлов  (как линии пересечения параллельных плоскостей). Но тогда одноименные углы Эйлера для различных полюсов будут равны друг другу в любой момент времени:

   , что и доказывает теорему.

3°. Матрица поворотов.

Возьмем в начальный момент  сопутствующие оси  совпадающими по направлению с соответствующими неподвижными осями , так что их ортами будут . Тогда ориентацию подвижных осей  (их ортов ) в рассматриваемый момент  можно получить из начальной  с помощью следующих трех поворотов: на угол  вокруг оси , затем на угол  вокруг оси  и, наконец, на угол  вокруг оси  (Рис.17).

При первом повороте орты  переходят в орты , связанные с исходными ортами преобразованиями

,    ,    .

Эти три равенства представимы матричной зависимостью

    ,       .

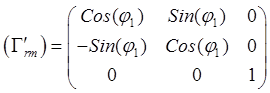При втором повороте орты  преобразуются в орты  в виде

    ,       .

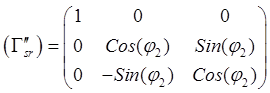Наконец, при третьем повороте орты  перейдут в орты  так, что

    ,       .

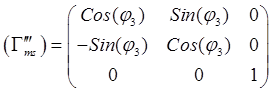Таким образом, орты  и  связаны преобразованием

    ,       ,                                                      (10.2)

матрица которого равна произведению трех предыдущих матриц и, следовательно, может быть выражена через эйлеровы углы:

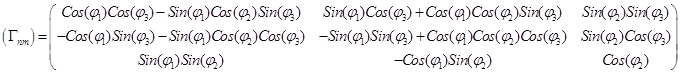. (10.3)

Таким образом, заданными эйлеровыми углами элементы -матрицы однозначно определяются. Обратно, задание - матрицы однозначно определяет эйлеровы углы. Действительно, в этом случае согласно (10.3) будем иметь равенства

,    ,    ,

,    , которые в интервалах

,    ,   

определяют углы Эйлера формулами

,    ;    ;

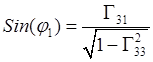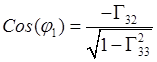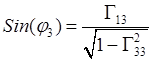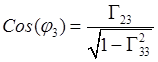,    .                                                                       (10.4)

Из условий ортонормированности элементов , а также и формул (10.2) следуют отношения

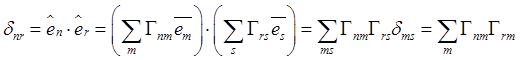, правые части которых с помощью транспонированной матрицы ,  можно представить в виде матричного произведения

   или   ,                                                                                       (10.5)

где , а  – единичная матрица. Отсюда следует, что трансформированная матрица совпадает с обратной матрицей: , т.е.  является ортогональной матрицей.

Элементам -матрицы можно придать определенный геометрический смысл. Из формул (10.2) следуют соотношения

,                                                                                                (10.6)

из которых ясно, что эти элементы совпадают с косинусами углов между подвижными и неподвижными осями.

4°. Уравнения движения точек тела.

Уравнения (10.1) движения твердого тела позволяют установить уравнения движения любой его точки. Сопутствующая система координат  неизменно связана с телом, поэтому тело в этой системе покоится. Это значит, что координаты  любой точки  тела в ней остаются неизменными во все время движения. Следовательно, тройкой чисел-координат  можно определять точку тела. Тем самым сопутствующая система координат позволяет не только устанавливать положение тела в пространстве, но и определять (индивидуализировать) точки тела.

Возьмем некоторую точку  тела и установим уравнения ее движения. Обозначим через  и  ее вектор-радиусы в неподвижной и в сопутствующей системах, а через – вектор-радиус полюса  (Рис.18). Тогда из векторного треугольника  будем иметь векторное уравнение движения этой точки

.                                                                 (10.2)

Для получения координатных уравнений движения точки представим входящие в (10.2) векторы в базисе системы отсчета. Имеем, очевидно,

,    ,    .

Здесь вектор  представлен в базисе сопутствующих осей, где точка  определена координатами .Для получения разложения этого вектора в системе отсчета, воспользуемся разложением (10.2) ортов  в базисе . Тогда для вектора  будем иметь 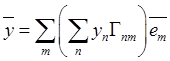 и (10.2) после подстановки в него разложений векторов примет вид

.

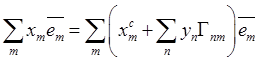Так как равные векторы в одном и том же базисе имеют равные компоненты, отсюда следуют зависимости