Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 50

В результате векторное уравнение  определяет тангенциальную реакцию  через известные силы  и :

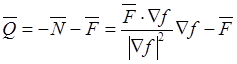.                                                                                           (28.6)

Рассмотрим далее случаи, когда положение равновесия заранее не известно и подлежит определению. Исследуем случаи гладкой и шероховатой поверхности.

а) Пусть поверхность гладкая, так что реакция нормальна к ней. В этом случае векторное уравнение равновесия (28.3) упрощается:

,                                                                                                            (28.7)

и в проекциях на оси декартовой системы  принимает вид

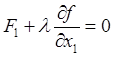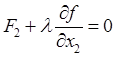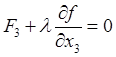,   ,   ,   .                               (28.8)

Эти уравнения позволяют определить положение равновесия на поверхности.

Действительно, исключив в (28.7) с помощью (28.5) множитель связи, получим векторное уравнение

, эквивалентное трем скалярным уравнениям для определения координат положений равновесия на поверхности

   .                                                                           (28.9)

Пусть, в частности, тяжелая точка  покоится на гладкой сфере радиуса  с центром в начале координат (Рис.65). Тогда будем иметь

,   ,

,   ,   ,

,   ,  

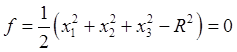и уравнения равновесия (28.8) имеют вид

, , , .

Первое, второе и четвертое уравнения определяют два положения равновесия

,   , которые совпадают с полюсами  и  сферы (Рис.66); третье уравнение определяет множитель связи

.

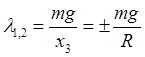Если учесть, что в данном случае градиент связи совпадает с вектор-радиусом точки:

, то нормальная реакция в положениях равновесия равна

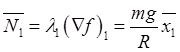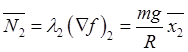,   , т.е. в положении равновесия  реакция  направлена в сторону вектор-радиуса , а в положении  реакция  противоположно  (Рис.66). При этом в обоих положениях равновесия модули реакций равны весу точки

.

б) Пусть поверхность шероховата. Тогда ее реакция имеет нормальную и тангенциальную составляющие, и уравнения равновесия точки на поверхности имеют общий вид (28.3):

,   ,   ,      .                                       (28.11)

Для определения положений равновесия исключим из них силу трения и множитель связи. Из уравнений равновесия, записанных в виде , следует равенство квадратов модулей его левой и правой частей, из которого ввиду  следуют равенства

,   .

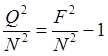Отсюда и из закона Кулона получаем выражения

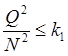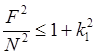,   .                                                                                                    (28.12)

Определив  из (28.5): 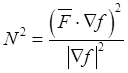, условие (28.12) представим через активную силу и уравнение поверхности

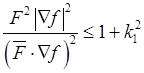.                                                                                                            (28.13)

Это неравенство выражает условие, которому должны удовлетворять координаты точки, покоящейся на поверхности. Отсюда следует, что положений равновесия оказывается бесконечное множество: они заполняют собою некоторую часть поверхности.

Если в (28.13) сохранить только знак равенства, то оно выразит уравнение некоторой поверхности:

,                                                                               (28.14)

которая, пересекаясь с поверхностью , определит линию , ограничивающую область равновесия.

Таким образом, влияние шероховатости поверхности проявляется в том, что вместо дискретных положений равновесия на поверхности появляются целые области равновесия.

Найдем для примера положения равновесия тяжелой точки  на шероховатой сфере радиуса  с центром в начале координат (Рис.67). В этом случае

,   ,   ,   ,

,   ,   ,

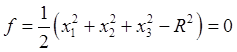и уравнение области равновесия на сфере (28.13) можно представить в одной из форм

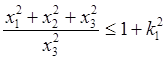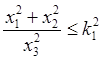,   ,   , где  – угол между вектор-радиусом и вертикалью: . Для границы области равновесия будем иметь . Отсюда получаем два угла

,   ,

,   .

Следовательно, границами области равновесия служат параллели , . Из условия равновесия  теперь ясно, что областями равновесия тяжелой точки на поверхности шероховатой сферы являются поверхности шаровых сегментов, примыкающих к полюсам.