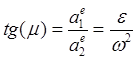Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 14

,           .                                              (9.33)

Из формул (9.24), (9.26) и (9.33) следует, что для знания уравнения движения точки по окружности, ее скорости и ускорения достаточно знать ее радиус и уравнение вращения радиуса

Рис.10

.

Глава2  Движение твердого тела.

В этой главе будут рассмотрены уравнения движения  твердого тела, изложены способы определения движения, скоростей и ускорений его точек, дано представление перемещения тела и исследованы частные случаи eго движения.

10. Уравнения движения тела и его точек.

1°. Обобщенные коорлинаты твердого тела.

Рис.15

Рассмотрим движение твердого тела  относительно системы отсчета . Для определения положения тела с ним связывают вспомогательную прямоугольную декартову систему  с базисными ортами . Начало  этой системы совпадает с некоторой точкой тела, называемой полюсом, а ее оси все время проходят в теле через одни и те же точки. Система координат  движется вместе с телом или, как еще говорят, сопутствует телу в его движении, поэтому ее называют подвижной или сопутствующей системой. Положение тела относительно системы отсчета полностью определяется положением системы , которое задается его координатами , а ориентация – эйлеровыми углами  (Рис.15). Последние выводятся следующим образом. Проведем через полюс оси  параллельно соответствующим осям  системы отсчета и обозначим через  линию пересечения плоскостей  и , называемую линией узлов. Угол  называют углом прецессии. Он изменяется при вращении тела вокруг оси  в пределах . Угол , изменяющийся при вращении тела вокруг линии узлов  в пределах , называют углом нутации. Наконец, угол  называют углом собственного вращения. Он изменяется при вращении тела вокруг оси  в пределах . Таким образом, шесть параметров  , определяющих положение тела в системе отсчета , называют обобщенными координатами тела.

2°. Уравнения движения твердого тела.

При движении твердого тела его положение в системе отсчета изменяется. Вместе с ним изменяются и обобщенные координаты тела. Зависимости

,                                                                                      (10.1)

называют уравнениями движения тела. Далее будем предполагать, что эти функции дважды непрерывно-дифференцируемы (т.е. принадлежат классу ).

Первые три уравнения  определяют движение тела вместе с полюсом при неизменной ориентации, а последние три  – изменение ориентации тела вокруг неподвижного полюса. Тем самым произвольное движение тела можно рассматривать как сложное: состоящее из движения вместе с полюсом и одновременного вращения вокруг полюса.

Рис.16

Полюс в теле выбирается произвольно. Если перейти от полюса  к полюсу , то уравнения движения полюса изменятся, ибо разные точки тела движутся вообще по-разному. Что касается вращений тела вокруг различных полюсов, то они оказываются одинаковыми. Именно, справедлива теорема: “Вращательная часть движения твердого тела не зависит от выбора полюса”.

Доказательство. Возьмем в теле два полюса  и. Снабдим штрихом все величины, относящиеся к полюсу  и, аналогично, двумя штрихами – величины, относящиеся к полюсу  (Рис.16). Оси  так же, как и оси , проводятся параллельно неподвижным осям  и, следовательно, они будут параллельны друг другу в любой момент времени:  . Что касается сопутствующих систем, то в некоторый момент их можно направлять в теле произвольно; во все же другие моменты их ориентировка зависит oт движения тела. Пользуясь этим, в начальный момент времени направим их параллельно друг другу:

при        .

Тогда, так как сопутствующие системы неизменно связаны с телом, они останутся параллельными в любой момент времени:

при любом        .