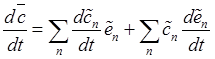 .
(18.2)
.
(18.2)
В первой сумме
правой части дифференцируются по времени только компоненты вектора в подвижных
осях, базисные же орты этих осей считаются постоянными. Следовательно, эта
сумма выражает изменение вектора относительно подвижных осей ![]() ; она обозначается через
; она обозначается через ![]() и называется относительной производной:
и называется относительной производной:
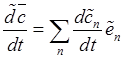 .
(18.3)
.
(18.3)
Во второй сумме
в правой части (18.2) дифференцируются только базисные орты ![]() , изменение со временем которых происходит
только за счет движения среды
, изменение со временем которых происходит
только за счет движения среды ![]() – переносного движения.
Если учесть формулы Пуассона
– переносного движения.
Если учесть формулы Пуассона 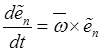 (
(![]() – угловая скорость среды), то эту сумму
можно записать в виде
– угловая скорость среды), то эту сумму
можно записать в виде
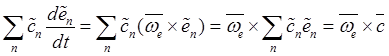 .
(18.4)
.
(18.4)
Эта сумма характеризует изменение вектора за счет переносного движения.
Подстановка (18.3), (18.4) в (18.2) дает связь между абсолютной и относительной производными вектора
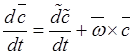 , т.е. абсолютное изменение вектора
складывается из относительного и переносного изменений.
, т.е. абсолютное изменение вектора
складывается из относительного и переносного изменений.
19. Сложное движение точки.
1°. Уравнения, скорость и ускорение точки в относительном движении.
Пусть тело ![]() является точечным телом
является точечным телом ![]() . Рассмотрим ее относительное движение,
т.е. движение в системе
. Рассмотрим ее относительное движение,
т.е. движение в системе ![]() , связанно со средой
, связанно со средой ![]() . При этом отвлекаемся от движения самой среды,
полагая ее “неподвижной”. Уравнения относительного движения в координатной и
векторной формах имеют вид
. При этом отвлекаемся от движения самой среды,
полагая ее “неподвижной”. Уравнения относительного движения в координатной и
векторной формах имеют вид
![]()
![]() ;
;
![]() .
(19.1)
.
(19.1)
Скорость и
ускорение точки по отношению к системе координат ![]() обозначают
через
обозначают
через ![]() и
и ![]() и
называют относительной скоростью и относительным ускорением. Относительная
скорость определяется как относительная производная по времени от вектора-радиуса
и
называют относительной скоростью и относительным ускорением. Относительная
скорость определяется как относительная производная по времени от вектора-радиуса
![]() :
:
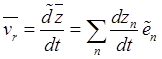 ,
(19.2)
,
(19.2)
![]() ,
, 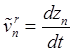
![]() .
.
А относительное ускорение – как относительная производная по времени от относительной скорости
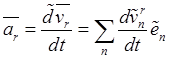 ,
,
![]() ,
, 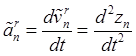 .
(19.3)
.
(19.3)
Таким образом, все характеристики относительного движения точки определяются по обычным правилам кинематики точки.
2°. Уравнения, скорость и ускорение точки в переносном движении.
Переносное
движение точки – движение среды ![]() в системе отсчета
в системе отсчета ![]() задается уравнениями движения полюса
задается уравнениями движения полюса ![]() среды и уравнениями ее вращения вокруг
полюса (эйлеровыми углами):
среды и уравнениями ее вращения вокруг
полюса (эйлеровыми углами):
![]() ,
, ![]() ,
, ![]() .
(19.4)
.
(19.4)
В результате
относительного движения точка ![]() последовательно совпадает
с различными точкам среды, которые движутся, вообще говоря, по-разному. Поэтому
переносной скоростью
последовательно совпадает
с различными точкам среды, которые движутся, вообще говоря, по-разному. Поэтому
переносной скоростью ![]() и переносным ускорением
и переносным ускорением ![]() точки
точки ![]() называют
скорость и ускорение той точки среды, с которой
точка
называют
скорость и ускорение той точки среды, с которой
точка ![]() в данный момент совпадает; поскольку среда
в данный момент совпадает; поскольку среда
![]() рассматривается как твердое тело, то эти
величины определяются в виде
рассматривается как твердое тело, то эти
величины определяются в виде
![]() ,
, ![]() ,
(19.5)
,
(19.5)
где ![]() –
относительный вектор-радиус точки
–
относительный вектор-радиус точки ![]() (Рис.38).
(Рис.38).
3°. Уравнения, скорость и ускорение точки в абсолютом движении.
Абсолютное
движение точки ![]() определяется ее уравнениями
(координатными и векторным) движения относительно неподвижной системы координат
определяется ее уравнениями
(координатными и векторным) движения относительно неподвижной системы координат
![]() :
:
![]()
![]() ;
; ![]() .
(19.6)
.
(19.6)
Скорость и ускорение
точки по отношению к неподвижной системе координат обозначается через ![]() и
и ![]() и
называются абсолютной скоростью и абсолютным ускорением. Абсолютная скорость
равна абсолютной производной по времени от абсолютного вектор-радиуса точки:
и
называются абсолютной скоростью и абсолютным ускорением. Абсолютная скорость
равна абсолютной производной по времени от абсолютного вектор-радиуса точки:
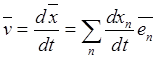 ,
(19.7)
,
(19.7)
![]() ,
, 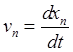
![]() .
.
Абсолютное ускорение равно абсолютной производной по времени от абсолютной скорости
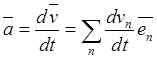 ,
,
![]() ,
, 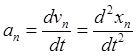
![]() .
(19.8)
.
(19.8)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.