Следовательно, производная от вектора скорости по криволинейной скорости равна производной от вектора-радиуса по соответствующей криволинейной координате.
Вычислим далее
производные ![]() и
и 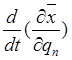 :
:
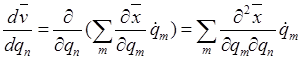 ,
,
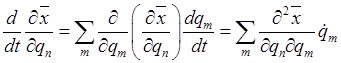 .
.
Сравнение этих соотношений приводит к равенству
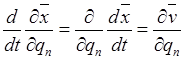 ,
(8.10)
,
(8.10)
т.е. дифференцирование вектор-радиуса по времени и по криволинейной координате можно менять местами.
С помощью равенств (8.9) и (8.10) физические компоненты ускорения (8.7) можно записать в виде
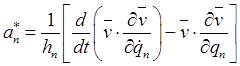 .
(8.11)
.
(8.11)
Представим теперь выражение в квадратной скобке через квадрат скорости. Имеем
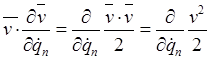 ,
, 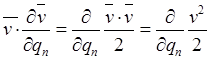 .
.
Подстановка этих выражений в (8.11) дает для физических компонент ускорения окончательные выражения
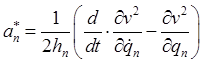 ,
, ![]() .
(8.12)
.
(8.12)
Входящий в (8.12) квадрат скорости через коэффициенты Ламе и криволинейные скорости выражается в виде
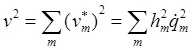 .
(8.13)
.
(8.13)
Подстановка (8.13) в (8.12) дает представление компонентов ускорений через коэффициенты Ламе, криволинейные скорости и ускорения
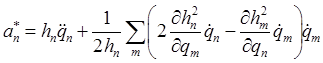 .
(8.14)
.
(8.14)
Модуль вектора
ускорения и его ориентация относительно элементов базиса в точке ![]() даются известными формулами
даются известными формулами
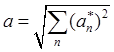 ,
, 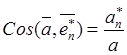 .
(8.15)
.
(8.15)
5°. Определение движения и скорости точки по ее ускорению и начальному состоянию.
Пусть заданы физические
компоненты ускорения точки в криволинейных координатах как непрерывные функции
времени ![]() и начальное состояние точки:
и начальное состояние точки: ![]() ,
, ![]() (коэффициенты
Ламе полагаются определенными выбранной системой). Тогда равенства (8.14),
записанные в виде системы, вместе с начальными условиями
(коэффициенты
Ламе полагаются определенными выбранной системой). Тогда равенства (8.14),
записанные в виде системы, вместе с начальными условиями
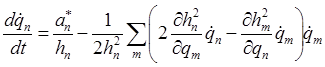 ,
, 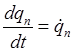 ,
(8.16)
,
(8.16)
![]() ,
, ![]() ,
, ![]()
образуют начальную задачу для
криволинейных координат и скоростей ![]() ,
, ![]() . Допущения о функциях
. Допущения о функциях ![]() ,
, ![]() обеспечивают
существование и единственность решения. Таким образом, задание ускорения точки и
ее начального состояния позволяет найти скорость точки и уравнения ее движения.
обеспечивают
существование и единственность решения. Таким образом, задание ускорения точки и
ее начального состояния позволяет найти скорость точки и уравнения ее движения.
6°. Движение корабля с постоянным курсовым углом.
Рассмотрим
задачу об определении траектории корабля, идущего под постоянным курсовым углом
![]() к географическому меридиану. Корабль
принимаем за точку
к географическому меридиану. Корабль
принимаем за точку ![]() , движущуюся по поверхности
земного шара. Движение корабля рассматриваем в сферических координатах
, движущуюся по поверхности
земного шара. Движение корабля рассматриваем в сферических координатах ![]() ,
, ![]() ,
, ![]() (
(![]() – радиус,
– радиус, ![]() – долгота,
– долгота, ![]() –
широта) (Рис.10), связанных с декартовыми координатами зависимостями
–
широта) (Рис.10), связанных с декартовыми координатами зависимостями
![]() ,
, ![]() ,
, ![]() .
.
Обратные зависимости имеют вид
![]() ,
, 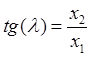 ,
, 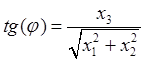 .
.
Как видно из последних формул,
координатными поверхностями ![]() ,
, ![]() ,
, ![]() служат
соответственно сфера, полуплоскость и конус, а координатными линиями –
служат
соответственно сфера, полуплоскость и конус, а координатными линиями – ![]() -линия – прямая (радиус),
-линия – прямая (радиус), ![]() -линия – окружность (параллель),
-линия – окружность (параллель), ![]() -линия – окружность (меридиан).
-линия – окружность (меридиан).
Выполнение условий
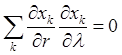 ,
, 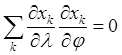 ,
,
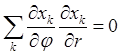
означает ортогональность сферических координат. Коэффициенты Ламе в сферической системе имеют значения
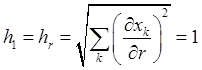 ,
, 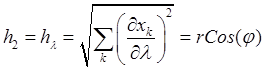 ,
, 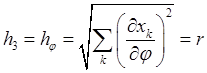 .
.
На поверхности
сферы скорость корабля имеет составляющие ![]() ,
, ![]() , направленные вдоль параллели и меридиана
соответственно. Из треугольника скоростей (Рис.10) находим
, направленные вдоль параллели и меридиана
соответственно. Из треугольника скоростей (Рис.10) находим
![]() .
.
Подставив в это равенство значения скоростей и разделив переменные, получим дифференциальное уравнение траектории
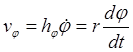 ,
,  ;
;
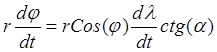 ;
; 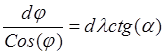 .
.
В последнем равенстве обе его части представимы в виде дифференциалов функций
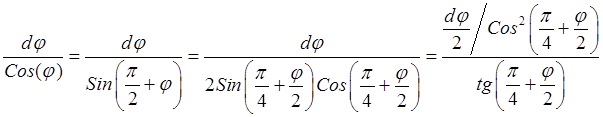 ,
,
![]()
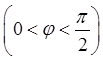 .
.
Подстановка в
уравнение этих выражений и интегрирование от начального положения корабля ![]() до рассматриваемого
до рассматриваемого ![]() дают уравнение траектории корабля
дают уравнение траектории корабля
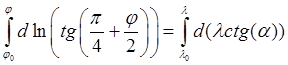 ,
, 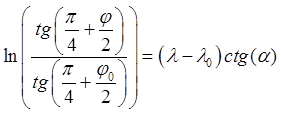 , или окончательно
, или окончательно
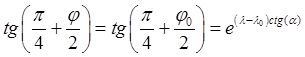 .
.
Эту кривую, принадлежащую поверхности сферы, называют локсодромией.
9. Естественное представление движения точки.
Движение точки можно определять без использования системы координат путем задания траектории и уравнения движения по траектории.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.