Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 49

   ,   ,

,   ,   ,   , а компоненты активной силы (силы тяжести), начальные координаты и скорости имеют значения

,   ,   ;

,   ,   ,

,   ,   .

Для решения задачи воспользуемся уравнениями (27.13), для гладкой поверхности

   ,   , имеющими в рассматриваемом случае вид

,   ,   ,   .

Третье из этих уравнений определяет множитель связи: , а первое и второе уравнения в результате интегрирования определяют общее уравнение в ви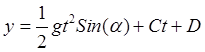де

,   , где  – произвольные постоянные. Начальными условиями эти постоянные определяются в виде

,   ,   ,   , поэтому уравнения движения точки по наклонной плоскости имеют вид

,   ,   .

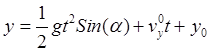Исключение из этих уравнений времени дает уравнение траектории в виде параболы, принадлежащей плоскости :

,   .

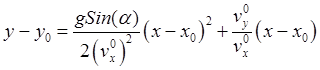Из выражения нормальной реакции  находим: , , т.е. реакция постоянна, ортогональна плоскости и направлена вдоль положительного направления оси .

28. Равновесие точки.

Рассмотрим равновесие свободной и несвободной точек и выясним условия, при которых оно реализуется.

1°. Равновесие свободной точки.

Частным видом движения материальной точки является ее равновесие. Говорят, что точка находится в равновесии относительно некоторой инерциальной системы координат, если ее положение в этой системе не изменяется со временем (или если ее скорость  в этой системе тождественно равна нулю):  (или ) . Условия реализации равновесия точки выражает теорема:

“Для равновесия первоначально покоившейся свободной точки необходимо и достаточно равенство нулю равнодействующей с приложенных сил”.

Необходимость. Пусть точка покоится: , в частности, . Тогда ее ускорение также будет нулевым , и из основного закона следует равенство нулю равнодействующей силы .

Достаточность. Пусть точка первоначально покоилась и равна нулю равнодействующая сила: , . Тогда основной закон  принимает вид . Отсюда следует интеграл . Поскольку , скорость будет тождественно нулевой: , и теорема тем самым доказана.

Заметим, что если , а , то , т.е. точка не будет покоиться, а будет совершать инерционное движение.

Итак, для покоящейся точки уравнение движения  принимает вид уравнения равновесия

.                                                                                                                                (28.1)

В декартовой системе координат  это векторное уравнение эквивалентно трем скалярным уравнениями равновесия, выражающим равенство нулю компонент силы

   .                                                                                                          (28.2)

В общем случае при равновесии точки силы зависят от координат: . Если они удовлетворяют условию

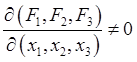, то уравнения (28.2) можно разрешить относительно координат и получить решение  , определяющее равновесие точки. Таким образом, уравнения равновесия позволяют по силам находить положение равновесия (одно или несколько).

2°. Равновесие несвободной точки

Пусть точка  покоится на поверхности  под действие активной силы, зависящей от координат . Тогда ее скорость и ускорение равны нулю: ,  и дифференциальные уравнения несвободного движения

,   ,   ,  

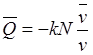принимают вид конечных уравнений равновесия на поверхности

,   ,   ,      .                                         (28.3)

Векторные уравнения (28.3) в декартовой системе координат  (Рис.65) эквивалентны следующей системе скалярных уравнений

,   ,   ,      .                   (28.4)

Эти уравнения позволяют решать различные задачи стесненного равновесия.

Пусть положение точки, совместное со связью, известно , . Тогда активная сила также известна:  и уравнения равновесия определяют реакцию. Действительно, первое уравнение в (28.3), записанное в форме , после скалярного умножения на  и учета условия  определяет множитель связи и, следовательно, нормальную реакцию

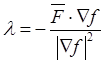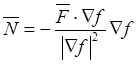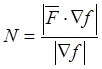,   ,   .                                                             (28.5)