Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 4

Рис.3

Когда время меняется, изменяется и вектор, а его конец описывает некоторую кривую, называемую годографом вектора. При этом само пространство  называют пространством годографа вектора . Зависимости

                                                                                                           (2.8)

называют параметрическими уравнениями годографа вектора, а уравнение (2.7) – векторным уравнением годографа.

3. Уравнения движения и траектория точки в декартовых координатах.

1°. Координатные уравнения движения и траектория.

Рассмотрим движение точки относительно прямоугольной декартовой системы отсчета , связанной с телом отсчета. Положение точки в этой системе определяется ее координатами  (Рис.4). При движении положение точки меняется со временем, поэтому функциями времени будут и ее координаты

             .         (3.1)

Рис.4

Зависимости (3.1) называют координатными уравнениями движения точки. Они в любой момент времени определяют положение точки относительно тела отсчета.

Принимается, что для достаточно гладких движений функции  однозначны и дважды непрерывно-дифференцируемы .

Точке  соответствуют проекции  на координатные оси. Из рис.3 видно, что . Следовательно, уравнение  определяет движение точки  вдоль оси . Поэтому согласно (3.1) можно считать, что движение точки в пространстве является результирующим трех составляющих движений вдоль координатных осей.

При движении точка переходит из одного положения в другое. Геометрическое место точек пространства, с которыми последовательно совпадает движущаяся точка, называется траекторией (Рис.4). Например, след, оставляемый реактивным самолетом в пространстве, определяет траекторию самолета. Уравнения движения точки (3.1) являются параметрическими уравнениями ее траектории.

2°. Векторное уравнение движения.

Уравнение движения можно представить в векторной форме. Каждой точке  пространства можно сопоставить вектор , начало которого совпадает с началом координат, а конец – с данной точкой: . Этот вектор называют вектор-радиусом точки  (Рис.4). Вектор-радиус можно рассматривать как векторную сумму векторов  (правило параллелепипеда): . Каждый из слагаемых векторов представляется через соответствующие координату и орт: . Поэтому для вектор-радиуса справедливо разложение

,                                                                                                                          (3.2)

показывающее, что он является функцией координат точки .

Дифференцированием этого равенства по координате можно получить представление через вектор-радиус элементов базиса

.

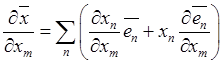Так как базисные векторы постоянны, а координаты точки независимы, справедливы соотношения

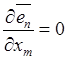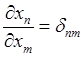,   , в силу которых предыдущее равенство принимает вид

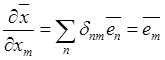,                                                                                                            (3.3)

т.е. элемент координатного базиса в точке вдоль какой-либо оси равен производной ее вектор-радиуса по соответствующей координате.

При движении точки ее вектор-радиус в силу (3.1) изменяется со временем

.                                                                                                           (3.4)

Эту зависимость называют векторным уравнением движения точки.

Легко видеть, что физическое пространство  является в то же время пространством годографа вектор-радиуса  (Рис.4), а годографом вектор-радиуса служит траектория точки.

4. Вектор скорости точки.

1°. Определение скорости по уравнению движения.