Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 8

Рис.9

Каждая пара координатных поверхностей пересекается вдоль некоторой линии, называемой координатной. В точке  пространства пересекаются три координатные линии (Рис.9). В произвольной системе координат координатные поверхности и линии являются вообще кривыми поверхностями и кривыми линиями, поэтому такую систему называют криволинейной, а сами координаты  криволинейными.

Криволинейные координаты определяют точку  пространства, поэтому функцией этих величин будет и вектор-радиус точки  (Рис.9). На  координатной поверхности эта координата фиксирована, а две другие изменяются, поэтому ее векторное уравнение имеет вид  (где индекс ). Наконец, на  координатной линии эта координата изменяется, а две другие – фиксированы, поэтому ее векторное уравнение будет вида .

2°. Ковариантный базис. Ортогональные системы.

С каждой точкой пространства можно связать тройку векторов , являющихся производными по координатам от ее вектор-радиуса

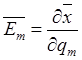
    .               (7.5)

Рис.10

При частном дифференцировании  по  эта координата изменяется, а две другие координаты ,  полагается фиксированными, т.е. точка  остается на -координатной линии, а производная  направлена по касательной к этой линии. Так как в точке пересекаются три линии, то в ней будет определена тройка векторов . Эти векторы во всех точках пространства некомпланарны. Действительно, объем  параллелепипеда, построенного на них как на ребрах (равный смешанному произведению векторов) ввиду условия (7.2) отличен от нуля

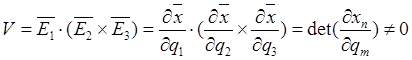, что и означает некомпланарность векторов. Это обстоятельство позволяет рассматривать векторы  в качестве координатного базиса, называемого ковариантным (Рис.10).

Криволинейную систему  называют ортогональной, если в каждой точке пространства координатные линии взаимно ортогональны. Поскольку каждый из векторов  идет по касательной к соответствующей координатной линии, то условие ортогональности последних имеет вид

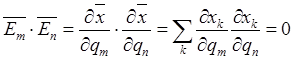
                  .                                    (7.6)

(Здесь учтено, что вектор-радиус имеет представление ).

Таким образом, ортогональность криволинейной системы выражается тремя равенствами, ограничивающими вид функции , определяющих криволинейную систему. В дальнейшем ограничимся рассмотрением только ортогональных координатных систем.

3°. Коэффициенты Ламе, ортонормированный базис.

Каждый вектор  представим в виде произведения его модуля  на единичный вектор – орт  направления, в котором он направлен: . Применяя это свойство к векторам ковариантного базиса, получим

.

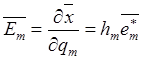Модули  этих векторов называют коэффициентами Ламе. Эти коэффициенты представимы через формулы (7.1), определяющие криволинейные координаты. Из соотношений

,        

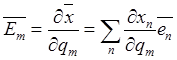
и определения коэффициентов находим

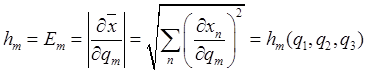.                                                                   (7.8)

Что касается ортов , то они коллинеарны элементам  ковариантного базиса и, следовательно, направлены по касательным к линиям в точке .

Тройка векторов , определенная в каждой точке  пространства образует ортонормированный координатный базис. Элементы этого базиса зависят от положения точки, представимы друг через друга и ортонормированны:

,    ,    .                                                       (7.9)

4°. Представление вектора в ортогональной системе.

Рассмотрим вектор  элементарного перемещения  точки . Дифференцируя равенство , получим разложение вектора  в ортонормированном координатном базисе

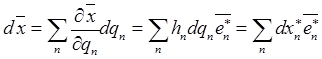.                                                                          (7.10)

Величины  называют физическими компонентами вектора .

Подобно (7.10) для любого вектора  можно рассматривать разложение в базисе :

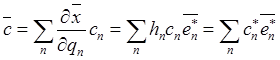,                                                                                   (7.11)

где величины  называют физическими компонентами вектора. Эти компоненты равны скалярным произведениям вектора на элементы базиса