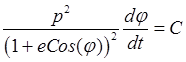 ,
, 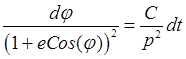 , откуда интегрированием получим
, откуда интегрированием получим
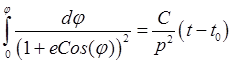 , (26.19)
, (26.19)
где ![]() –
момент прохождения через перицентр.
–
момент прохождения через перицентр.
Для
эллиптического движения (![]() ) подынтегральную
функцию можно преобразовать посредством подстановки
) подынтегральную
функцию можно преобразовать посредством подстановки
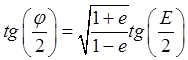 ,
(26.20)
,
(26.20)
тогда будем иметь
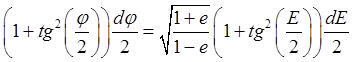 ,
, 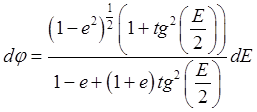 ,
,
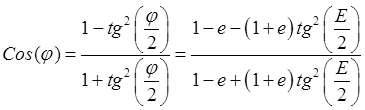 ,
, 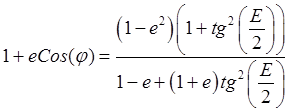 ,
,
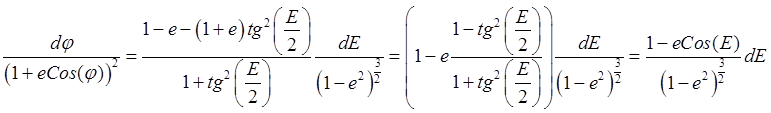 .
.
Вычисляя в (26.19) интеграл по
переменной ![]() в пределах от
в пределах от ![]() до
до ![]() , получим
, получим
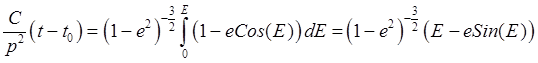 , или в окончательном виде
, или в окончательном виде
![]() ,
, 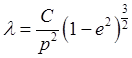 .
(26.21)
.
(26.21)
Это равенство называют уравнением
Кеплера. Оно устанавливает зависимость ![]() , а
согласно (26.20) – зависимость
, а
согласно (26.20) – зависимость ![]() , что совместно с ранее
установленными формулами
, что совместно с ранее
установленными формулами ![]() ,
, ![]() полностью определяет движение.
полностью определяет движение.
Из уравнения
Кеплера следует зависимость между периодом ![]() обращения
планеты вокруг Солнца
обращения
планеты вокруг Солнца ![]() и большой полуосью эллипса.
Действительно, пусть в момент
и большой полуосью эллипса.
Действительно, пусть в момент ![]() планета находилась в
перицентре
планета находилась в
перицентре ![]() , для которого
, для которого ![]() и
согласно (26.20)
и
согласно (26.20) ![]() . Тогда после полного оборота в
момент
. Тогда после полного оборота в
момент ![]() будем иметь
будем иметь ![]() и
и ![]() . Подставив эти значения
. Подставив эти значения ![]() и
и ![]() в
уравнение (26.20), с учетом
в
уравнение (26.20), с учетом ![]() получим
получим
![]() ,
, 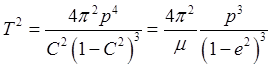 .
.
Для эллипса параметр и
эксцентриситет определяются полуосями ![]() и
и ![]() в виде
в виде 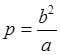 ,
, 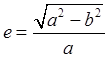 . Следовательно,
. Следовательно,
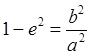 ,
, 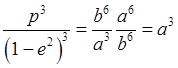
и формула для квадрата периода принимает вид
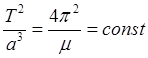 ,
(26.22)
,
(26.22)
так как Гауссова постоянная
Солнца ![]() не зависит от параметров планет. Формула
(26.22) выражает третий закон Кеплера: “Квадраты звездных времен обращения
планет вокруг Солнца пропорциональны кубам больших полуосей их орбит”.
не зависит от параметров планет. Формула
(26.22) выражает третий закон Кеплера: “Квадраты звездных времен обращения
планет вокруг Солнца пропорциональны кубам больших полуосей их орбит”.
Третий закон Кеплера имеет приближенный характер. Он установлен в предположении неподвижности притягивающего центра. Если учесть движение этого центра, то получим уточненный вид этого закона
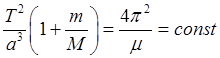 ,
(26.23)
,
(26.23)
где ![]() и
и ![]() – массы планеты и Солнца. Так как для
планет
– массы планеты и Солнца. Так как для
планет 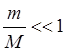 (масса наибольшей из планет – Юпитера не
превышает одной тысячной массы Солнца), то отличие невелико. Пренебрегая этим
отличием, из (26.23) получим третий закон в обычной форме (26.22).
(масса наибольшей из планет – Юпитера не
превышает одной тысячной массы Солнца), то отличие невелико. Пренебрегая этим
отличием, из (26.23) получим третий закон в обычной форме (26.22).
Глава Динамика несвободной точки.
Материальное тело всегда движется в окружении других тел, с которыми оно взаимодействует. В частном случае взаимодействие осуществляется при касании тел друг друга. При этом ограничиваются возможности движения тела – оно становится несвободным (а движение – стесненным). Особенности стесненного движения и рассматриваются в этой главе.
27. Движение точки по поверхности.
Законы движения свободной и несвободной точки, как показывает опыт, вообще различны. В этом параграфе устанавливается вид основного закона при движении точки по поверхности.
1°. Геометрическая связь.
Пусть точка во все время движения остается на поверхности некоторого тела. В этом случае говорят, что точка движется по поверхности. Эта поверхность ограничивает свободу перемещения точки (связывает движение), и поэтому ее называют связью.
Допустим, что
движение рассматривается относительно инерциальной системы отсчета ![]() . Тогда поверхности тела соответствует
некоторое уравнение
. Тогда поверхности тела соответствует
некоторое уравнение
![]() или
или ![]() ,
(27.1)
,
(27.1)
называемое уравнением связи. Связь
(27.1), уравнение которой содержит только координаты точки, называют
геометрической; ей соответствует неподвижная поверхность. Примером такой связи
может служить сфера радиуса ![]() с центром в начале
координат:
с центром в начале
координат:
![]()
2°. Ограничения на скорость и ускорение.
При движении
точки ![]() вдоль поверхности ее координаты,
меняющиеся со временем
вдоль поверхности ее координаты,
меняющиеся со временем ![]() , в каждый момент должны
удовлетворять уравнению поверхности
, в каждый момент должны
удовлетворять уравнению поверхности
![]() ,
(27.2)
,
(27.2)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.