Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 11

1°. Геометрия линии.

Рис.11

Пусть в системе отсчета  задана линия . Рассмотрим некоторые ее свойства. Возьмем на линии некоторую точку  за начало отсчета дуг. Тогда положение любой точки линии можно определить длиной дуги , отсчитываемой от  до точки  и считаемой положительной в одну сторону от точки  и отрицательной в другую (Рис.11). Длина дуги , взятая с надлежащим знаком, является дуговой координатой точки .

В системе отсчета линию  можно задать параметрическими или векторным уравнениями

                ,            ,                                                           (9.1)

где принято, что функции  (трижды непрерывно-дифференцируемы).

Введем естественный базис в каждой точке линии.

Рассмотрим первую и вторую производные по дуге от вектор-радиуса и выясним их геометрический смысл. Первую производную обозначим через

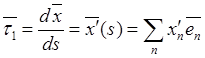                                                                                                     (9.2)

Линия  является годографом вектор-радиус, поэтому вектор  направлен по касательной к  в сторону возрастания дуги. Модуль  равен единице:

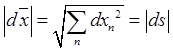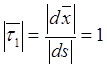,      , то есть  является ортом касательной.

Вторую производную  представим через модуль  и орт :

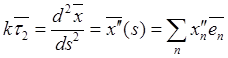.                                                                                               (9.3)

Дифференцированием по дуге равенства  и последующим использованием (9.2), (9.3) находим

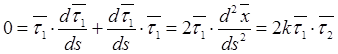,        , т.е.  является ортом нормали , называемой главной нормалью.

Нормаль, ортогональную к главной нормали, называют бинормалью; ее орт обозначают через . Этот вектор можно представить в виде векторного произведения

.

Таким образом, в каждой точке линии определены три единичных взаимоортогональных вектора , , , направленные соответственно по касательной, главной нормали и бинормали, которые образуют естественный базис (Рис.11). Элементы естественного базиса переменны, представимы друг через друга и ортонормированны:

,      ,      .                                                                 (9.4)

Элементы базиса определяют естественные оси линии: орт  – касательную , орт – главную нормаль , орт  – бинормаль . Каждая пара элементов базиса определяет естественную плоскость: орты ,  – соприкасающуюся плоскость , орты ,  – нормальную плоскость , орты ,  – спрямляющую плоскость  (Рис.11). Все три элемента базиса определяют естественный трехгранник .

При смещении точки  вдоль линии элементы естественного базиса изменяют ориентацию в пространстве. Темп этого изменения выражается формулами Френе

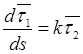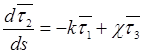,      ,      ,                                                             (9.5)

допускающими компактную запись через вектор Дарбу :

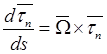
        ,                .                                                     (9.6)

В окрестности каждой точки линия  отклоняется и от направления прямой линии, и от направления плоской линии. Отклонение от прямой называют искривленностью, а ее меру – кривизной . Отклонение от плоскости называют искривленностью, а ее меру – кручением . Обратные им величины 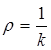,  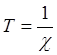называют соответственно радиусами кривизны и кручения. При задании линии параметрическими уравнениями (9.1) кривизна и кручение определяются следующими из (9.3) и (9.5) формулами

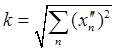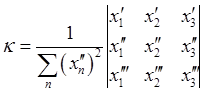,     .                                                                       (9.7)

Пусть в типичной точке  линии приложен вектор . Для него справедливо разложение в естественном базисе (правило параллелепипеда)

.                                                                                                                          (9.8)

Коэффициенты  в этом разложении называют естественными компонентами вектора. По этим компонентам с привлечением свойства ортонормированности (9.4) модуль и направление вектора определяются формулами

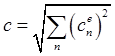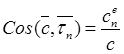
,            .                                                              (9.9)

2°. Естественное задание движения точки.