Согласно теореме кинетический момент точки вокруг центра или оси изменяется только в том случае, когда действует соответствующий силовой момент.
В частности, когда, например, ![]() , то из третьего в (30.12) равенства
следует интеграл площадей:
, то из третьего в (30.12) равенства
следует интеграл площадей:
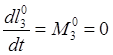 ,
, ![]() ,
, ![]() .
.
То есть, при отсутствии силового момента вокруг третьей оси кинетический момент точки вокруг этой оси сохраняет постоянное значение.
Теорему (30.10) можно представить в интегральной форме. Разделяя в этом равенстве дифференциалы и интегрируя в соответствующих пределах, получим
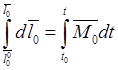 ,
, ![]() ,
(или
,
(или ![]() ,
, ![]() ),
(30.13)
),
(30.13)
т.е. приращение кинетического момента точки за какой-либо промежуток времени равно импульсу силового момента за тот же промежуток. При этом кинетический и силовой моменты должны определяться относительно одного и того же неподвижного центра.
5°. Изменение кинетической энергии.
При движении
точки ее кинетическая энергия изменяется со временем: ![]() .
Темп этого изменения выражает теорема о кинетической энергии:
.
Темп этого изменения выражает теорема о кинетической энергии:
“В каждый момент времени скорость изменения кинетической энергии равна мощности действующей силы”
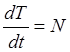 .
(30.14)
.
(30.14)
Доказательство. Возьмем основной закон динамики в векторной форме и умножим скалярно обе его части на вектор скорости:
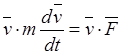 . (30.15)
. (30.15)
Тогда
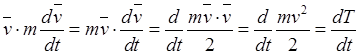 ,
,
![]() .
.
Подстановка этих выражений в
(30.15) приводит к равенству ![]() , совпадающему с
(30.14). Теорема доказана.
, совпадающему с
(30.14). Теорема доказана.
Согласно теореме (30.14) кинетическая энергия точки изменяется только в том случае, когда отлична от нуля мощность действующей силы.
Подобно теоремам о количестве движения и о кинетическом моменте теорема о кинетической энергии позволяет получить интеграл дифференциальных уравнений движения (интеграл энергии) при определенном условии на действующую силу.
Сила ![]() называется потенциальной, если взятому со
знаком “минус” градиенту некоторой скалярной функции
называется потенциальной, если взятому со
знаком “минус” градиенту некоторой скалярной функции ![]() (называемой
потенциальной энергией):
(называемой
потенциальной энергией):
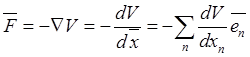 ,
, 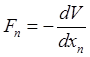
![]() .
(30.16)
.
(30.16)
Условие потенциальности силы выражает теорема:
“Для потенциальности силы ![]() , являющейся непрерывно дифференцируемой
функцией координат, необходимо и достаточно выполнение условий
, являющейся непрерывно дифференцируемой
функцией координат, необходимо и достаточно выполнение условий
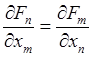
![]() ”.
(30.17)
”.
(30.17)
Действительно, пусть сила потенциальна, тогда
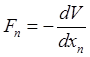
![]() .
(30.18)
.
(30.18)
Дифференцированием этого
равенства по координате ![]() , устанавливаем условия
(30.17):
, устанавливаем условия
(30.17):
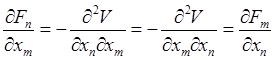 ;
;
Необходимость, таким образом, обоснована.
Для
доказательства достаточности условий (30.17) покажем, что при их выполнимости
можно найти такую функцию ![]() , для которой
выполняются равенства (30.18).
, для которой
выполняются равенства (30.18).
Для этого проинтегрируем первое
равенство 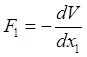 по
по ![]() от
от ![]() до
до ![]() ,
считая
,
считая ![]() ,
, ![]() фиксированными
параметрами:
фиксированными
параметрами:
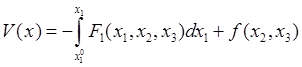 .
(30.19)
.
(30.19)
Найденная функция при всякой ![]() удовлетворяет первому условию в (30.18).
Функцию
удовлетворяет первому условию в (30.18).
Функцию ![]() можно выбрать так, чтобы удовлетворялись и
два других. Действительно, дифференцируя (30.19) по параметру
можно выбрать так, чтобы удовлетворялись и
два других. Действительно, дифференцируя (30.19) по параметру ![]() и пользуясь заданным условием
и пользуясь заданным условием 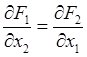 , получим
, получим
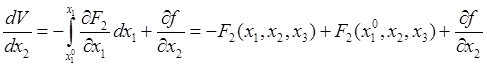 .
.
Правая часть этого равенства
будет равна ![]() , если положить
, если положить
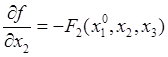 или
или 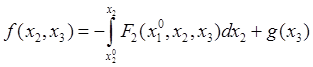 .
.
Следовательно, согласно (30.19) функция
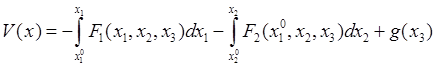 (30.20)
(30.20)
при любом ![]() удовлетворяет
двум первым условиям в (30.18).
удовлетворяет
двум первым условиям в (30.18).
При определенном выборе ![]() можно удовлетворить и третьему из них.
Действительно, дифференцируя (30.20) по
можно удовлетворить и третьему из них.
Действительно, дифференцируя (30.20) по ![]() и
полагая согласно (30.17)
и
полагая согласно (30.17) 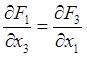 ,
, 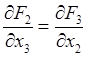 , будем иметь
, будем иметь
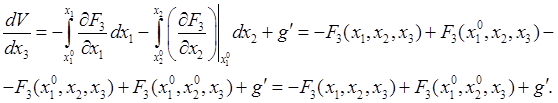
Поставленная цель будет достигнута, если принять
![]() , или
, или 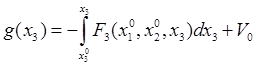 ,
, ![]() .
.
Таким образом, при выполнении условий (30.17) потенциальной энергией будет функция (30.20):
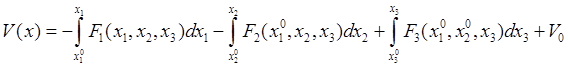 . (30.21)
. (30.21)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.