Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 56

Рассмотрим точку  массы , движущуюся под действием силы  относительно неинерциальной системы отсчета , связанной с движущейся средою  (Рис.73), и установим основной закон динамики в этом движении.

Примем, что уравнения движения среды  (твердого тела) в неподвижной (инерциальной) системе отсчета  заданы:

,      .                (31.1)

Из них первые три уравнения определяют скорость и ускорение полюса :

,   ,          (31.2)

а последние три – угловую скорость и угловое ускорение среды:

,   .                                                                           (31.3)

Будем исходить из абсолютного движения точки в инерциальной системе  (связанной с основным телом отсчета ), которое определяется законом Ньютона

.                                                                                                                  (31.4)

С помощью кинематических формул ,  этому закону можно придать вид дифференциального уравнения второго порядка для абсолютного вектор-радиуса :

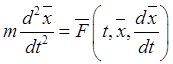.                                                                                                        (31.5)

Заменим в законе (31.4) абсолютное ускорение через относительное, переносное и добавочное ускорения согласно теореме Кориолиса

и оставим в левой части равенства только первое слагаемое (перенеся другие слагаемые в правую часть):

.

Введя затем обозначения

,

,                                                                                                    (31.6)

этому уравнению придадим вид

.                                                                                                  (31.7)

Векторы ,  подобно обычным силам имеют силовую размерность и могут быть измерены динамометром, поэтому их называют силами инерции.

Вектор  называют переносной силой инерции; он равен по величине произведению массы точки на переносное ускорение и направлен против этого ускорения.

Вектор  называют кориолисовой силой инерции; он равен по величине произведению массы на кориолисово ускорение и направлен против этого ускорения.

Поскольку движение среды задано, то векторы  согласно (31.2) и (31.3) являются известными функциями времени, поэтому силы инерции (31.6) зависят от переменных , характеризующих состояние относительного движения

,   .                                                                                            (31.8)

Функцией этих переменных можно представить и обычную силу.

Сила , определяющая взаимодействие точки с другими телами (движение которых полагается известным), зависит, точнее говоря, не от абсолютного положения  и абсолютной скорости  точки, а от относительного расположения и от относительной скорости взаимодействующих тел. Относительное положение двух тел (точек  и ) определяется разностью вектор-радиусов , а относительная скорость – разностью скоростей (точек  и )  в одном и том же положении. Следовательно,

.

Используя связи абсолютных и относительных вектор-радиусов и скоростей

,   ;   ,   , для разностей вектор-радиусов и скоростей получим выражения

,   , которые не зависят от системы отсчета. Отсюда следует, что от системы отсчета не зависит и сила:

                                                            (31.9)

и ее можно представить как функцию переменных :

.                                                                                                      (31.10)

Следовательно, уравнению (31.7) можно придать вид, аналогичный уравнению (31.4):

,

.                                                                      (31.11)

Если еще воспользоваться кинематическими формулами

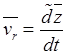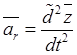,   , то (31.11) можно записать в виде дифференциального уравнения второго порядка для относительного вектор-радиуса , аналогичного уравнению (31.5):

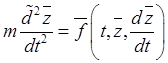.                                                                                                       (31.12)