2°. Определение закона изменения силы.
Формулы (24.2)
позволяют вычислить силу в любой момент времени, но они не содержат информации
о физической природе силы, то есть о законе изменения силы. Чтобы получить этот
закон, т.е. найти силу как функцию переменных ![]() и
и ![]() , мало, оказывается, задания одного
движения точки; требуется наряду с массой
, мало, оказывается, задания одного
движения точки; требуется наряду с массой ![]() задавать
достаточно широкий класс движений, а именно, движение, зависящее от шести
произвольных параметров:
задавать
достаточно широкий класс движений, а именно, движение, зависящее от шести
произвольных параметров:
![]()
![]() .
(24.4)
.
(24.4)
Будем считать, что эти функции дважды непрерывно дифференцируемы и таковы, что отличен от нуля определитель
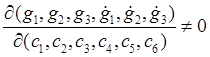 . (24.5)
. (24.5)
Тогда, действуя вышеизложенным способом, получим для компонент силы выражения, зависящие от времени и шести параметров
![]() .
(24.6)
.
(24.6)
Рассмотрим систему шести уравнений, состоящую из (24.4) и следующих уравнений, полученных дифференцированием (24.4) по времени
![]() ,
, ![]() , и будем рассматривать ее как
систему неявных функций относительно параметров
, и будем рассматривать ее как
систему неявных функций относительно параметров ![]() . Условие
(24.5) обеспечивает разрешимость этой системы относительно параметров. Фактически
разрешая систему, получим зависимости
. Условие
(24.5) обеспечивает разрешимость этой системы относительно параметров. Фактически
разрешая систему, получим зависимости
![]()
![]() .
.
Внося эти выражения параметров в (24.6), получим компоненты, а также закон изменения силы в виде
![]() ,
, ![]() .
(24.7)
.
(24.7)
Полученные формулы решают задачу. Таким образом, задача нахождения силы по движению решается всегда и сводится к выполнению дифференциальных и алгебраических операций.
3°. Вывод закона Гука.
В качестве
примера решения прямой задачи динамики определим силу, обуславливающую
колебательные движения точки. Пусть для точки массы ![]() задано
шести параметрическое семейство колебаний
задано
шести параметрическое семейство колебаний
![]()
![]() ,
(24.8)
,
(24.8)
в которых роль параметров играют
амплитуды ![]() и начальные фазы
и начальные фазы ![]() (частота
(частота
![]() является заданным числом); установим закон
изменения действующей силы.
является заданным числом); установим закон
изменения действующей силы.
Дифференцированием по времени уравнений (24.8) находим скорости и ускорения:
![]() ,
, ![]() , следовательно, компоненты
действующей силы по основному закону динамики определятся в виде
, следовательно, компоненты
действующей силы по основному закону динамики определятся в виде
![]() ,
, ![]() .
(24.9)
.
(24.9)
Из (24.9) следует исключить параметры путем выражения их через время, координаты и скорости точки. Однако для этой цели не требуется определять каждый из параметров, а достаточно воспользоваться уравнениями колебаний (24.8), чтобы найти входящие в (24.9) их комбинации.
В результате для компонент силы получаем формулы
![]()
![]() , определяющие саму силу в виде
закона Гука:
, определяющие саму силу в виде
закона Гука:
![]() .
(24.10)
.
(24.10)
Согласно
(24.10) колебания точки обуславливаются силой, пропорциональной отклонению ![]() от равновесного положения
от равновесного положения ![]() и направленной против отклонения. Эту
силу называют силой упругости. С такой силой, в частности, действует на точку
деформированная пружина, при этом коэффициент
и направленной против отклонения. Эту
силу называют силой упругости. С такой силой, в частности, действует на точку
деформированная пружина, при этом коэффициент ![]() определяет
так называемую жесткость пружины, а
определяет
так называемую жесткость пружины, а ![]() – величину деформации
пружины.
– величину деформации
пружины.
25. Определение движения по силе и начальному состоянию.
1°. Постановка обратной задачи.
Рассмотрим
решение обратной задачи динамики точки на основе декартовых дифференциальных
уравнений. Пусть известен закон изменения силы, действующей на точку массы ![]() , и ее начальное состояние; и требуется
найти движение точки. Это означает, что заданы декартовы компоненты силы как
функции времени, координат и скоростей
, и ее начальное состояние; и требуется
найти движение точки. Это означает, что заданы декартовы компоненты силы как
функции времени, координат и скоростей
![]()
![]() ,
(25.1)
,
(25.1)
причем предполагается, что эти компоненты являются непрерывными функциями всех аргументов и принадлежат классу Липшица по координатам и скоростям
![]() по
по ![]() ;
; ![]() по
по ![]() (25.2)
(25.2)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.