Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 43

Действующая сила  непрерывна по времени и непрерывно дифференцируема по координате. Тем самым начальная задача (25.16) однозначно разрешима.

Уравнение (25.16) – линейное неоднородное, поэтому его общее решение складывается из общего решения  однородного уравнения и частного решения  неоднородного: . Решение  можно взять в виде , а решение   ищем в виде

,   ,   ,   .

Подстановка ,  в (25.16) приводит к уравнению

, которое удовлетворяется при .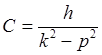

Таким образом, общее решение уравнения (25.16) имеет вид

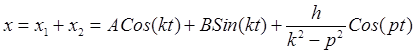.                                                  (25.17)

Отсюда следует, что скорость точки равна

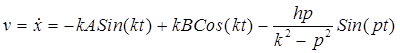.                                                         (25.18)

Полагая в (25.17), (25.18)  и используя начальные условия (25.16), получаем уравнения для постоянных

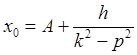,   , определяющие их в виде

,   .

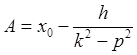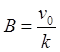Таким образом, уравнение движения (25.17) принимает вид

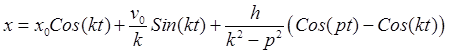.                                              (25.19)

Вводя вместо 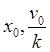 величины  согласно формулам (25.15), равенство (25.19) можно представить в виде суперпозиции трех колебаний

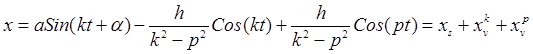.                             (25.20)

Здесь слагаемое  описывает собственное колебание, а  и  – вынужденные колебания (вызванные возмущающей силой) с собственной частотой  и частотой силы  соответственно. Исследуем последнее из них.

При , , при , , поэтому  можно записать в виде

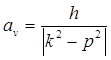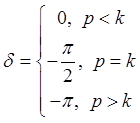,   ,   ,                                               (25.21)

где у вынужденных колебаний  – амплитуда, а  – начальная фаза. Обозначим через  сдвиг фаз, равный разности фазы силы  и фазы колебания : . Поведение величин  и  в зависимости от частоты силы  иллюстрируют графики (Рис.56 и 57). Из графиков видно, что эти величины являются разрывными функциями.

Из графика для  видно также, что амплитуда вынужденных колебаний при  (т.е. при малых частотах возмущающей силы) конечна, при  (т.е. при больших частотах силы) она близка к нулю, а при  неограниченно возрастает. Явление резкого возрастания амплитуды вынужденных колебаний при частоте возмущающей силы, близкой к частоте собственных колебаний, называется резонансом. При резонансе возмущающая сила действует “в такт” с собственными колебаниями, что приводит к наиболее сильному раскачиванию точки. Из графика для сдвига фаз  видно, что при  фазы колебаний и силы совпадают, при  фазы противоположны, и при  фазы сдвинуты на . Покажем справедливость последнего заключения.

Рассмотрим полное вынужденное колебание

.

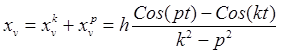При резонансе  это колебание становится неопределенным: 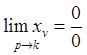. Раскрывая неопределенность, находим

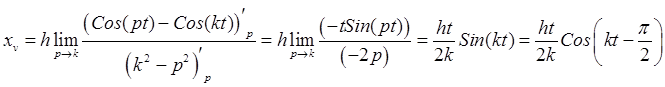, т.е. в случае резонанса

,   ,   .

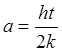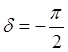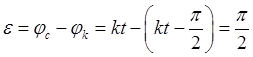Характер поведения амплитудных кривых и вынужденного колебания при резонансе показан на Рис.58. Из графика видно, что амплитуда вынужденных колебаний неограниченно возрастает со временем.

Заметим, что при учете силы сопротивления вида ,  можно показать, что функции  вместо разрывных становятся непрерывными, поведение которых показано на Рис.59.

26. Движение под действием силы тяготения.

К числу обратных задач динамики относится и задача о движении точки под действием силы тяготения, которая является важной задачей небесной механики. Решение ее дает картину движения точки около притягивающего центра, в частности, движение искусственного спутника.

1°. Секторная скорость.

Рассмотрим вначале понятие секторной скорости, используемое в дальнейшем изложении. При движении точки по траектории ее вектор-радиус  ометает некоторую поверхность (Рис.60). Ведем величину, характеризующую темп изменения площади этой поверхности.

Пусть в близкие моменты времени  точка занимает положения  на траектории с вектор-радиусами . За время  вектор-радиус получает приращение , а площадь поверхности – приращение , приближенно равное площади треугольника , которую можно выразить в виде . Величину , равную отношению площади по времени