![]() .
(13.4)
.
(13.4)
Выразим
угловую скорость через ее модуль ![]() и орт
и орт ![]() :
: ![]() . Тогда
. Тогда ![]() , где
, где ![]() –
проекция
–
проекция ![]() на направление
на направление ![]() , и
первое слагаемое в правой части (13.4) равно
, и
первое слагаемое в правой части (13.4) равно
![]() ,
, ![]() .
.
Так как ![]() ,
то последний член в (13.4) равен
,
то последний член в (13.4) равен ![]() . Следовательно,
равенство (13.4) принимает вид
. Следовательно,
равенство (13.4) принимает вид
![]() .
(13.5)
.
(13.5)
Разложим теперь
вектор ![]() на составляющую
на составляющую ![]() вдоль
угловой скорости и составляющую
вдоль
угловой скорости и составляющую![]() , ортогональную к ней
, ортогональную к ней ![]() , тогда
, тогда ![]() и
формула (13.5) принимает вид
и
формула (13.5) принимает вид
![]() .
(13.6)
.
(13.6)
 Это ускорение представляет собою нормальное
ускорение точки
Это ускорение представляет собою нормальное
ускорение точки ![]() при ее вращении вокруг вектора
угловой скорости, проведенного из полюса. Оно направлено от точки
при ее вращении вокруг вектора
угловой скорости, проведенного из полюса. Оно направлено от точки ![]() к мгновенной оси вращения (Рис.26b), поэтому его называют осестремительным ускорением.
к мгновенной оси вращения (Рис.26b), поэтому его называют осестремительным ускорением.
Внося (13.3) и (13.6) в (13.2), получаем равенство
![]() , выражающее следующую теорему
Ривальса:
, выражающее следующую теорему
Ривальса:
“В произвольном движении твердого тела ускорение любой его точки равно векторной сумме полюсного, вращательного и осестремительного ускорений” (Рис.26с).
2°. Вычисление ускорения точки тела.
Для вычисления вектора ускорения получим выражения его компонент. Ускорение (13.2) с учетом (13.4) запишем в виде
![]() .
(13.8)
.
(13.8)
В подвижном базисе ![]() входящие в (13.8) векторы представляются в
виде
входящие в (13.8) векторы представляются в
виде
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
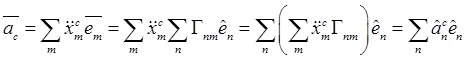 , поэтому согласно (13.8)
компоненты ускорения в подвижных осях равны
, поэтому согласно (13.8)
компоненты ускорения в подвижных осях равны
![]() (индекс
(индекс ![]() ). (13.9)
). (13.9)
Здесь ![]() –
задаваемые величины (определяющие точку
–
задаваемые величины (определяющие точку ![]() тела),
тела), ![]() – компоненты
угловой скорости, определяемые формулами Эйлера,
– компоненты
угловой скорости, определяемые формулами Эйлера, 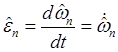 –
компоненты углового ускорения, а
–
компоненты углового ускорения, а ![]() – компоненты ускорения
полюса. Все эти величины определяются по уравнениям движения тела
– компоненты ускорения
полюса. Все эти величины определяются по уравнениям движения тела ![]() .
.
Компоненты
(13.9) определяют модуль ускорения и его ориентацию относительно подвижных осей
![]() в виде
в виде
![]() ,
, 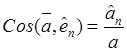 .
(13.10)
.
(13.10)
Ускорение
точки можно вычислить и по его компонентам в неподвижном базисе. Представляя
векторы из (13.8) в базисе ![]() , получим
, получим
![]() ,
, ![]() , ,
, , ![]() ,
, ![]() ,
,
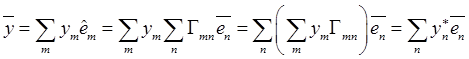 , тогда компоненты ускорения (13.8)
в неподвижных осях будут равны
, тогда компоненты ускорения (13.8)
в неподвижных осях будут равны
![]() (индекс
(индекс ![]() ). (13.11)
). (13.11)
Здесь ![]() –
компоненты ускорения полюса,
–
компоненты ускорения полюса, ![]() – компоненты угловой скорости, определяемые по формулам
Эйлера,
– компоненты угловой скорости, определяемые по формулам
Эйлера, ![]() – компоненты углового ускорения, а
– компоненты углового ускорения, а ![]() – компоненты вектора
– компоненты вектора ![]() . Все эти величины определяются по
уравнениям движения тела
. Все эти величины определяются по
уравнениям движения тела ![]() .
.
По компонентам
(13.11) модуль ускорения и его ориентация относительно неподвижных осей ![]() определяются формулами
определяются формулами
![]() ,
, 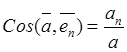 .
(13.12)
.
(13.12)
Рассмотрим частные случаи движения тела.
14. Поступательное движение тела.
Движение твердого тела называют поступательным, если любая прямая, связанная с телом, остается параллельной самой себе во все время движения.
Поступательное движение совершают, например, кузов вагона на прямолинейном участке пути, ступенька эскалатора метрополитена и т.п. Это одно из простейших и весьма распространенных движений тела.
1°. Уравнения поступательного движения.
![]() При поступательном движении тела оси сопутствующей системы
координат
При поступательном движении тела оси сопутствующей системы
координат ![]() как прямые, связанные с телом остаются
параллельными самим себе. Следовательно, углы Эйлера при этом движении остаются
постоянными:
как прямые, связанные с телом остаются
параллельными самим себе. Следовательно, углы Эйлера при этом движении остаются
постоянными: ![]()
![]() . Без ограничения
общности можно принять, что в начальный момент времени эти оси были параллельны
соответствующим неподвижным осям. Тогда в начальный момент эйлеровы углы
равнялись нулю. Следовательно, они будут нулевыми и в любой другой момент:
. Без ограничения
общности можно принять, что в начальный момент времени эти оси были параллельны
соответствующим неподвижным осям. Тогда в начальный момент эйлеровы углы
равнялись нулю. Следовательно, они будут нулевыми и в любой другой момент: ![]()
![]() . Уравнения же движения
полюса
. Уравнения же движения
полюса ![]() сохраняют общий вид
сохраняют общий вид ![]()
![]() . Таким образом,
уравнения поступательного движения тела имеют вид
. Таким образом,
уравнения поступательного движения тела имеют вид
![]() ,
, ![]()
![]() .
(14.1)
.
(14.1)
Итак, в поступательном движении тело движется вместе с полюсом и не вращается вокруг полюса.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.