Необходимость.
Пусть точка покоится: ![]() , тогда
, тогда
![]() ,
, 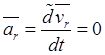 ,
, ![]()
и уравнение относительного
движения (31.11) ![]() дает второе условие в (31.17):
дает второе условие в (31.17): ![]() .
.
Достаточность.
Пусть выполнены условия (31.17), тогда уравнение относительного движения ![]() принимает вид
принимает вид ![]() или
или
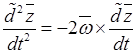 .
.
После скалярного умножения этого
равенства на ![]() получаем интеграл:
получаем интеграл:
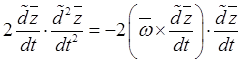 ,
, 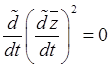 ,
, 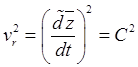 , где
, где ![]() –
произвольная постоянная. В силу начального условия
–
произвольная постоянная. В силу начального условия ![]() . Следовательно,
. Следовательно,
![]() . Теорема доказана.
. Теорема доказана.
Второе из
равенств в (31.17) называют векторным уравнением относительного равновесия. В
подвижной системе координат ![]() оно эквивалентно
системе трех уравнений
оно эквивалентно
системе трех уравнений
![]()
![]() ,
(31.18)
,
(31.18)
называемых уравнениями относительного равновесия точки в декартовых координатах. При выполнении условия
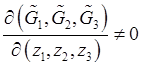
их можно разрешить
относительно координат ![]() и тем самым найти положение
равновесия (одно или несколько), в которых точка будет покоиться.
и тем самым найти положение
равновесия (одно или несколько), в которых точка будет покоиться.
32. Относительное движение у поверхности Земли.
Известно, что гелиоцентрическая система отсчета (связанная с центром Солнца) является инерциальной системой с высокой степенью точности. Геоцентрическая же система отсчета, имеющая начало в центре Земли и жестко с нею связанная, не является инерциальной системой в силу движения Земли по орбите и вращения вокруг своей оси. Рассмотрим некоторые особенности движения точки в этой неинерциальной системе.
1°. Уравнение движения. Вес тела.
![]() Пусть
Пусть ![]() – инерциальная
гелиоцентрическая система отсчета, связанная с Солнцем
– инерциальная
гелиоцентрическая система отсчета, связанная с Солнцем ![]() .
Свяжем с Землей
.
Свяжем с Землей ![]() – средой
– средой ![]() – геоцентрическую (неинерциальную) систему
– геоцентрическую (неинерциальную) систему
![]() , совместив начало
, совместив начало ![]() с
центром Земли, ось
с
центром Земли, ось ![]() – с земной осью и проведя оси
– с земной осью и проведя оси ![]() ,
, ![]() в
плоскости экватора (Рис.74). Будем рассматривать в этой системе относительное
движение точки
в
плоскости экватора (Рис.74). Будем рассматривать в этой системе относительное
движение точки ![]() массы
массы ![]() у
поверхности Земли. Обозначим через
у
поверхности Земли. Обозначим через ![]() и
и ![]() силы притяжения точки Землей
силы притяжения точки Землей ![]() и Солнцем
и Солнцем ![]() и через
и через
![]() – равнодействующую всех прочих сил (например,
реакцию связи, сопротивление среды и т.п.), тогда динамическое уравнение
относительного движения, согласно (31.11), будет
– равнодействующую всех прочих сил (например,
реакцию связи, сопротивление среды и т.п.), тогда динамическое уравнение
относительного движения, согласно (31.11), будет
![]() .
(32.1)
.
(32.1)
Пусть ![]() – угловая скорость вращения Земли.
Известно, что эта скорость постоянна и численно равна
– угловая скорость вращения Земли.
Известно, что эта скорость постоянна и численно равна
![]() ,
, ![]() об/сут
об/сут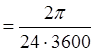 р/с
р/с![]() р/с.
р/с.
Тогда угловое ускорение у Земли
будет отсутствовать: ![]() , и переносная сила инерции
будет представлена суммой двух составляющих
, и переносная сила инерции
будет представлена суммой двух составляющих
![]() ,
(32.2)
,
(32.2)
где ![]() –
полюсная сила инерции, а
–
полюсная сила инерции, а ![]() – центробежная сила
инерции. Внося силу (32.2) в уравнение (32.1), будем иметь
– центробежная сила
инерции. Внося силу (32.2) в уравнение (32.1), будем иметь
![]() .
(32.3)
.
(32.3)
Обозначим
через ![]() массу Солнца и через
массу Солнца и через ![]() – вектор-радиусы точек
– вектор-радиусы точек ![]() и
и ![]() в
гелиоцентрической системе
в
гелиоцентрической системе ![]() . При движении в
окрестности Земли модуль относительного вектор-радиуса имеет порядок земного
диаметра
. При движении в
окрестности Земли модуль относительного вектор-радиуса имеет порядок земного
диаметра ![]() :
: ![]() и он
несравненно меньше расстояния
и он
несравненно меньше расстояния ![]() от Земли до Солнца:
от Земли до Солнца: ![]() . Поэтому в векторной сумме
. Поэтому в векторной сумме ![]() вторым слагаемым допустимо пренебречь
сравнительно с первым и с высокой степенью точности принять
вторым слагаемым допустимо пренебречь
сравнительно с первым и с высокой степенью точности принять ![]() . В этом приближении сила притяжения точки
. В этом приближении сила притяжения точки
![]() Солнцем будет равна
Солнцем будет равна
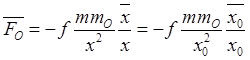 .
(32.4)
.
(32.4)
Запишем
уравнение движения Земли массы ![]() в гелиоцентрической
системе
в гелиоцентрической
системе ![]() под действием силы притяжения к Солнцу
под действием силы притяжения к Солнцу
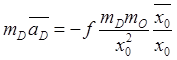 .
.
Умножив это
равенство на отношение ![]() и приняв во внимание
(32.4), для силы притяжения к Солнцу (32.4) получим представление
и приняв во внимание
(32.4), для силы притяжения к Солнцу (32.4) получим представление
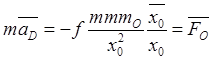 .
.
Теперь легко
видеть, что в (32.3) силы ![]() и
и ![]() взаимно уравновешиваются:
взаимно уравновешиваются:
![]() ;
(32.5)
;
(32.5)
обозначив еще через ![]() равнодействующую сил
равнодействующую сил ![]() и
и ![]() :
:
![]() ,
(32.6)
,
(32.6)
можно записать (32.3) в виде
![]() .
(32.7)
.
(32.7)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.