Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 25

Это уравнение распадается на уравнения двух совпадающих прямых, проходящих через начало :

,    .                                                                  (16.27)

Действительно, из уравнения (16.25) окружности находим

,   .

Подстановка этого значения  в уравнения прямых (16.27):

,

приводит каждое из них к одному и тому же виду

.

Таким образом, точки фигуры, принадлежащие окружности , описывают прямые линии, проходящие через начало координат.

17. Вращение твердого тела вокруг неподвижной оси.

Если при движении твердого тела расстояние всех его точек до двух неподвижных центров остаются неизменными, то движение называют вращением вокруг неподвижной оси, проходящей через эти центры.

Вращение вокруг неподвижных осей совершают, например, роторы турбин и электромоторов, маятник часов, маховик двигателя и т.п.

Вращательное движение является частным случаем сферического движения и соответствует случаю, когда из трех эйлеровых углов два угла имеют фиксированные значения. Вращение тела вокруг неподвижной оси является весьма распространенным движением. Наряду с поступательным движением, оно относится к числу простейших движений тела.

1°. Уравнение вращательного движения тела.

Пусть при движении тела сохраняются неизменными расстояния его точек до неподвижных центров  и , которые можно считать точками тела. Возьмем центр О за начало неподвижной системы координат  и направим ось  по прямой , а оси  и  – ортогонально к  и друг к другу так, чтобы получилась правая система отсчета (Рис.35). Точку О возьмем также за полюс (). Тогда в системе отсчета  полюс будет покоиться: . Установим, далее, вид уравнений вращения тела вокруг полюса.

Сопутствующую систему  выберем так, чтобы в некоторый начальный момент она совпадала с неподвижной системой . Тогда в любой другой момент времени согласно определению вращательного движения оси  и  будут совпадать, так что угол нутации будет равен нулю: . При этом два другие угла  и  будут изменяться вокруг одной и той же оси, а плоскости  и  совпадут друг с другом; положение линии узлов  становится неопределенным. Возьмем линию  совпадающей с осью ; тогда будем иметь ,  и уравнения вращения вокруг полюса примут вид , . Таким образом, уравнения вращательного движения тела вокруг неподвижной оси имеют вид

;   ,   .                                                                     (17.1)

Это движение описывается одним уравнением, выражающим изменение со временем угла собственного вращения.

2°. Уравнения движения и траектории точек вращающегося тела.

Во вращательном движении , поэтому матрицы поворотов, соответствующие прецессии и нутации являются единичными ,  и результирующая матрица поворотов совпадает с матрицей собственного вращения

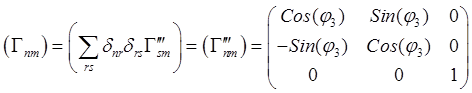.(17.2)

Общие уравнения движения типичной точки  тела

на основании (17.1) и (17.2) упрощаются и принимают вид

,    ,    .                             (17.3)

Установим форму траектории точки вращающегося тела. Из геометрических соображений следует, что постоянство расстояний точки  до центров и  означает, что точка должна находиться одновременно на сферах с центрами в точках  и  и радиусами . Следовательно, траекторией  будет линия пересечения сфер, т.е. окружность, плоскость которой ортогональна оси вращения, а центр лежит на этой оси (Рис.35) . Эти результаты следуют также из уравнений движения (17.3). Действительно, возведем в квадрат первое и второе равенства и сложим результаты. В итоге получим соотношение, свободное от . Присоединяя к нему последнее уравнение движения, будем иметь

,    .                                                                                              (17.4)

Первое из этих равенств является уравнением прямого кругового цилиндра с осью  и радиусом ,а второе – уравнением плоскости, ортогональной оси .

Траектория точки, представляющая собою линию пересечения этих поверхностей, является, окружностью  с центром на оси вращения и плоскостью, ортогональной этой оси. Радиус окружности равен , т.е. совпадает с расстоянием точки до оси вращения (Рис.35).