Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 29

4°. Сложение движений точки.

Пусть дано относительное и переносное движения точки , т.е. заданы ее уравнения движения относительно среды  (19.1) и уравнения движения самой среды (19.4). Тогда, беря уравнения переносного движения точки  среды

,    , где  – матрица поворотов, определенная углами , и подставляя в них уравнения относительного движения: , будем иметь

,   .                                                     (19.9)

Полученные уравнения позволяют определить положение точки  относительно неподвижной системы  в любой момент времени, поэтому они являются уравнениями ее абсолютного движения.

Таким образом, по относительному и переносному движениям точки можно установить ее абсолютное движения. Подобная задача называется сложением движений.

Аналогично решается обратная задача (задача разложения движений), в которой по заданным абсолютному и переносному движениям точки отыскивается ее относительное движение.

5°. Зависимость между скоростями точки в сложном движении.

Если точка одновременно участвует в двух движениях: относительном и переносном, то между скоростями составляющих и результирующего движений существует определенная связь, устанавливаемая следующей теоремой сложения скоростей.

Теорема: Если точка совершает сложное движение, то в каждый момент времени ее абсолютная скорость равна векторной сумме переносной и относительной скоростей:

.                                                                                                                       (19.10)

Доказательство. Пусть точка  совершает сложное движение. Рассмотрим ее абсолютный и относительный вектор-радиусы  и вектор-радиус полюса  среды . Пользуясь правилом сложения векторов, запишем векторное уравнение ее абсолютного движения в виде (Рис.39)

.                                                          (19.11)

Беря абсолютную производную по времени от этого равенства, находим

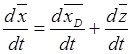.                                                             (19.12)

Если воспользоваться определением скорости точки и связью между абсолютной и относительной производными по времени, то будем иметь

,    ,   

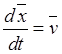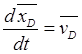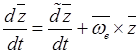
( – угловая скорость среды) и равенство (19.12) можно представить в виде

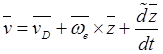.                                                                                                        (19.13)

В правой части этого равенства сумма двух первых векторов определяет переносную скорость точки , а последний вектор – относительную скорость

,    .

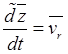Следовательно, равенство (19.13) представимо в виде , что и доказывает теорему.

Равенство (19.10) геометрически означает, что абсолютная скорость является замыкающей ломаной линии, звеньями которой являются переносная и относительная скорости (правило треугольника скоростей (Рис.41)).

Из этого представления следует, что для определения модулей скоростей и углов между ними можно пользоваться тригонометрическими методами. В частности, если известны модули переносной и относительной скоростей и угол  между ними, то модуль абсолютной скорости определяется по теореме косинусов в виде

.

Для аналитического определения абсолютной скорости достаточно определить ее компоненты, например, в подвижных осях . Из (19.10) находим

                                                    (19.14)

Здесь

,   , где  определяются по уравнениям относительного движения (19.1),  – по кинематическим формулам Эйлера через уравнения переносного движения (19.4), а  находятся по формулам (используя (19.4)):

, в которых матрица поворотов  определяется углами  обычными формулами.

Компонентами (19.14) модуль и направление абсолютной скорости по отношению к подвижной системе  определяются в виде

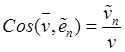,    .                                                                              (19.15)

6°. Движение капли дождя.

В качестве применения теоремы сложения скоростей рассмотрим движение капли дождя в безветренную погоду. В этом случае капля  падает на землю вертикально со скоростью . Пусть по горизонтальной дороге идет пешеход  с зонтом со скоростью . Под каким углом  к вертикали он должен держать рукоятку зонта для наилучшей защиты от дождя (Рис.42).