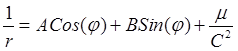Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 45

,   ,   , где  – произвольные постоянные.

Вводя вместо  другие постоянные  и переобозначая последнее слагаемое

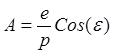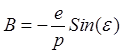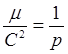,   ,   ,                                                                    (26.13)

получим уравнение конического сечения

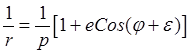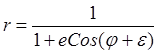,   ,                                                               (26.14)

в котором постоянная  является параметром,  – эксцентриситетом, а  – начальной фазой. Формула (26.14) выражает второй закон Кеплера: “Орбиты планет суть канонические сечения, в одном из фокусов которых находится Солнце”.

Конкретный вид орбиты зависит от значений постоянных  и ; постоянная  характеризует расположение орбиты относительно полярной оси. Выразим постоянные интегрирования через начальные условия.

Выражение скорости в полярных координатах

, преобразованное с помощью интеграла площадей:

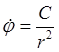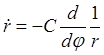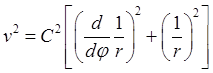,   ,   , позволяет получить начальные значения обратного радиуса и его производной по углу

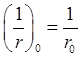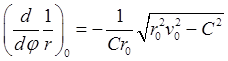,                                                                           (26.15)

(минус перед корнем соответствует тому, что знаки , а, следовательно, и  одинаковы). Подставив эти данные в выражения обратного радиуса (26.14) и его производной по углу, будем иметь

,   .

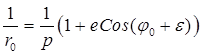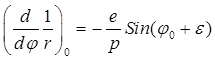Заменяя в равенствах параметр  и производную  согласно формулам (26.13) и (26.15), получим систему уравнений

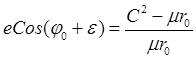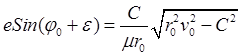,   , откуда  и  определяются в виде

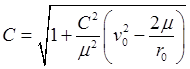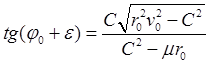,   .                                                    (26.16)

В частности, , если начальные величины связаны между собою условием (в дальнейшем считающимся выполненным)

.

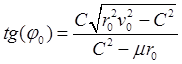В этом случае уравнение орбиты (26.14) принимает более простой вид

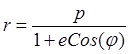.                                                                                                               (26.17)

Отсюда, в частности, видно, что при , , т.е. полярная ось пересекает орбиту в точке, ближайшей к притягивающему центру, называемой перицентром (при движении вокруг Солнца перицентр называют перигелием, а при движении вокруг Земли – перигеем).

Выражение (26.16) для эксцентриситета позволяет установить тип орбиты точки в зависимости от ее начального состояния:

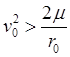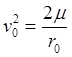при ,  , орбита – гипербола, при ,  , орбита – парабола, при 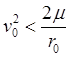,  , орбита – эллипс.

Чтобы точка могла неограниченно удаляться от притягивающего центра, ее начальная скорость должна быть не меньше параболической: .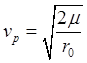

Выясним условия, при которых реализуется круговая орбита. Чтобы точка двигалась по кругу , ее эксцентриситет должен равняться нулю: . С учетом выражения (26.16) это условие приводит к уравнению

.

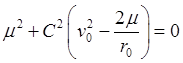Внося в него значение постоянной площадей согласно (26.10) равное , получим квадратное уравнение для :

.                                                                 (26.18)

Корни уравнения имеют комплексные значения

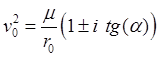, следовательно, движение по окружности при произвольном начальном состоянии невозможно. Чтобы это движение имело место, требуется вещественность корней, т.е. выполнение условия ; , либо . Следовательно, начальная скорость должна быть ортогональной начальному радиусу. Величина же начальной скорости при движении по кругу согласно (26.18) должна иметь значение 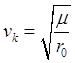 (эту скорость называют круговой). Формы орбит точки указаны на Рис.62.

Круговую и параболическую скорости называют также первой и второй космическими скоростями. При движении вокруг Земли (м/с², м) они имеют значения км/с, км/с.

Заметим, что при движении по кругу , т.е. в каждой точке полная скорость совпадает с круговой скоростью  и из закона площадей (26.10) вытекает, что движение в этом случае должно быть равномерным:

,   .

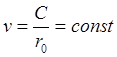4°. Уравнение движения по орбите.

При известной орбите, т.е. зависимости , для нахождения движения точки в плоскости  достаточно установить зависимость от времени полярного угла . С этой целью обратимся к интегралу площадей (26.10): . Заменяя в нем величину  ее значением из уравнения орбиты (26.17) и разделяя переменные, последовательно найдем