Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 23

Наряду с точкой  рассмотрим точку , являющуюся ее проекцией на плоскость . Векторы-радиусы этих точек  имеют разложения

,

и связаны между собою соотношением (Рис.30)

,   ,                                      (16.6)

Легко видеть, что первые два уравнения движения точки  будут тe же, что и у точки  в (16.5), а третье уравнение имеет вид . Это значит, что  совершает движение в плоскости  такое же, как и точка  в плоскости . Отсюда следует, что все точки тела, принадлежащие перпендикуляру к плоскости , движутся одинаково и таким образом, как движется точка . Следовательно, движение всего тела будет установлено, если будет известно движение в плоскости  плоской фигуры , являющейся проекцией тела на плоскость  (Рис.30). В этом аспекте уравнения движения тела (первая группа трех уравнения в (16.3)) являются уравнениями движения плоской фигуры : первые два уравнения ,  суть уравнения движения полюса  в плоскости , а третье уравнение  есть уравнение вращения фигуры  вокруг полюса  в этой плоскости.

3°. Скорости точек тела в плоском движении.

В плоском движении тела углы прецессии и нутации равны нулю: , поэтому  и угловая скорость тела принимает значение

   ,                                                                            (16.7)

Таким образом, при плоском движении тела вектор угловой скорости направлен ортогонально плоскости  движения плоской фигуры .

Рассмотрим скорость точки тела. Общее выражение скорости с учетом выражений (16.6) и (16.7) для векторов  и  принимает вид

,   .                                          (16.8)

Т.е. скорость точки тела совпадает со скоростью точки  плоской фигуры . Последняя же складывается из скорости полюса , общей для всех точек фигуры, и вращательной скорости , происходящей вследствие вращения фигуры вокруг полюса (Рис.32).

Для вычисления скорости установим выражения ее компонент в подвижных и неподвижных осях. Согласно (16.8) компоненты скорости в подвижных осях равны

,   ,   .                             (16.9)

Согласно формулам Эйлера (16.6) и (16.7) компоненты угловой скорости имеют значения

,   ,

;     , а компоненты скорости полюса с учетом (16.3) и (16.4) определяются формулами :

,    ,    .

Таким образом, компоненты (16.8), модуль и направление скорости относительно подвижных осей равны

, , ;            (16.10)

,         ,  ,  .

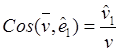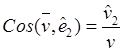Аналогично, согласно (16.8) компоненты скорости в неподвижных осях равны

,   ,   .                           (16.11)

Здесь согласно формулам Эйлера и уравнениям (16.3)

,

,

,

,   ,   , а компоненты вектора  в неподвижных осях в силу представления 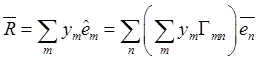 равны :

,,.

Таким образом, компоненты (16.11), модуль и направление скорости относительно неподвижных осей выражаются формулами

, , ;      (16.12)

,         ,  ,  .

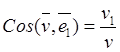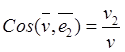Формулы (16.10) (или (16.12)) показывают, что скорость точки тела лежит в плоскости ее движения.

4°. Ускорения точек тела в плоском движении.

Для определения ускорения точки тела в плоском движении установим вначале выражение вектора углового ускорения  тела в этом случае. Согласно определению вектора  и (16.7) имеем

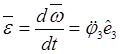
      .                                                                                            (16.13)

Следовательно, в плоском движении тела векторы угловой скорости и углового ускорения параллельны друг другу и ортогональны плоскости движения.

Рассмотрим ускорение точки тела. Общее выражение для ускорения точки согласно теореме Ривальса представимо в виде

.                                                                                                      (16.14)

Ввиду коллинеарности векторов угловой скорости и углового ускорения имеем

.                                                                                                         (16.15)

Из (16.14) следует, что ускорения точек  и  (Рис.30) совпадают друг с другом. В (16.14) вектор  есть ускорение полюса фигуры , а векторы ,   суть касательное и нормальное ускорения точки  при вращении фигуры  вокруг полюса.