т.е. векторное равенство (23.1) эквивалентно трем скалярным равенствам (23.2).
В кинематике установлено, что компоненты скорости и ускорения определяются через декартовы координаты точки формулами
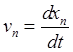 ,
, 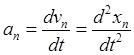 ,
, ![]() .
.
Подставляя эти выражения в (23.2) и обозначая
![]() , получим дифференциальные
уравнения движения точки в декартовых координатах
, получим дифференциальные
уравнения движения точки в декартовых координатах
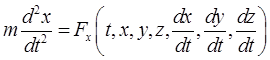 ,
,
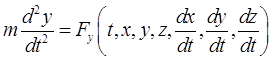 ,
(23.3)
,
(23.3)
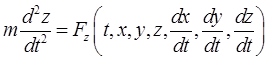 .
.
Эти уравнения образуют замкнутую
систему трех уравнений второго порядка для трех функций времени ![]() .
.
Замкнутую систему уравнений, описывающую некоторое явление, называют математической моделью явления. С этой точки зрения система уравнений (23.3) определяет в декартовых координатах математическую модель “материальная точка”.
2°. Дифференциальные уравнения в цилиндрических координатах.
Пусть с телом
отсчета связана ортогональная цилиндрическая система координат ![]() с ортонормированным базисом
с ортонормированным базисом ![]() . Разложим векторы
. Разложим векторы ![]() ,
входящие в закон (23.1), в этом базисе
,
входящие в закон (23.1), в этом базисе
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Из закона ![]() получим
три соотношения, выражающие равенство соответствующих физических компонентов
равных векторов
получим
три соотношения, выражающие равенство соответствующих физических компонентов
равных векторов ![]() и
и ![]() :
:
![]() ,
,
![]() ,
(23.4)
,
(23.4)
![]() .
.
С учетом кинематических формул и
представления вектор-радиуса ![]() имеем равенства
имеем равенства
![]()
![]()
позволяющие записать соотношения (23.4) в виде дифференциальных уравнений движения точки в цилиндрических координатах
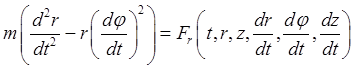 ,
,
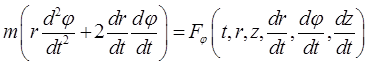 ,
(23.5)
,
(23.5)
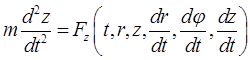 .
.
Эти уравнения образуют замкнутую
систему трех дифференциальных уравнений второго порядка для трех функций
времени: ![]() .
.
3°. Естественные дифференциальные уравнения движения точки.
Наряду с
координатными дифференциальными уравнениями движения точки, можно получить ее
естественные дифференциальные уравнения, связанные с естественным способом
представления движения. В естественном способе движение точки определяется
зависимостями от дуги ![]() кривизны
кривизны ![]() ,
кручения
,
кручения ![]() и времени
и времени ![]() :
:
![]() .
(23.6)
.
(23.6)
Из них первые две функции определяют естественные уравнения траектории, а последняя – уравнение движения по траектории. Из основного закона динамики можно получить уравнения для нахождения этих функций тем же путем, что и координатные уравнения.
Рассмотрим
естественный базис траектории ![]() (орты касательной,
главной нормали и бинормали) и представим в нем векторы
(орты касательной,
главной нормали и бинормали) и представим в нем векторы ![]() ,
входящие в закон
,
входящие в закон ![]() :
:
![]() ,
, ![]() ,
, ![]() ,
, ![]()
(Здесь и далее естественные компоненты векторов отмечены штрихами).
Согласно закону должны равняться друг другу соответствующие естественные компоненты равных векторов:
![]()
![]() .
(23.7)
.
(23.7)
Используем для естественных компонент скорости и ускорения известные формулы и переобозначим компоненты вектор-радиуса и силы
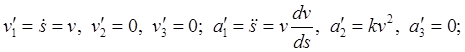
![]() ,
(23.8)
,
(23.8)
тогда динамические уравнения (23.7) можно записать в виде следующих естественных уравнений
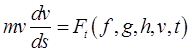 ,
,
![]() ,
(23.9)
,
(23.9)
![]() .
.
Естественные
уравнения составляют систему трех уравнений (одного дифференциального и двух
конечных) и содержат шесть неизвестных функций дуги ![]() :
: ![]() , тем самым они замкнутую систему не
образуют; кроме того, они не содержат кручения
, тем самым они замкнутую систему не
образуют; кроме того, они не содержат кручения ![]() –
составной части кинематических уравнений (23.6).
–
составной части кинематических уравнений (23.6).
Для замыкания системы установим дополнительные уравнения. Будем исходить из представления скорости
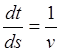 ,
(23.10)
,
(23.10)
и естественных компонент вектор-радиуса, а также орта касательной и формул Френе
![]() ,
, 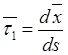 ,
,
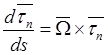 ,
, ![]()
![]() .
.
Дифференцирование по дуге первой группы равенств и использование остальных соотношений дает
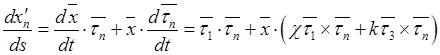
![]() .
.
Используя соотношения
![]() ,
, ![]()
![]() , инд.
, инд.![]() , запишем эту систему в развернутом
виде
, запишем эту систему в развернутом
виде
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.