Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 26

3°. Угловая скорость и угловое ускорение вращающегося тела.

Из уравнений  в (17.1) следуют равенства , в силу которых угловая скорость тела совпадает со скоростью собственного вращения, направлено по оси  вращения тела (Рис.35):

    .                                                                   (17.5)

Угловое ускорение тела, равное производной по времени от вектора его угловой скорости, также направлено по оси вращения и совпадает с ускорением собственного вращения

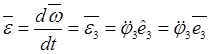
    .                                                                              (17.6)

Таким образом, во вращательном движении тела вокруг неподвижной оси угловая скорость и угловое ускорение тела параллельны друг другу. Эти результаты согласуются с введенными в круговом движении точки понятиями угловой скорости и углового ускорения радиуса точки.

4°. Скорости и ускорения точек вращающегося тела.

При вращательном движении тела общее выражение для скорости типичной точки  тела

                                                                                                                     (17.7)

совпадает с ее обычным значением при круговом движении. Действительно, в данном случае скорость полюса  (совпадающего с началом ) равна нулю: , а вращательная скорость  может быть преобразована.

Представляя вектор  в виде суммы двух векторов: , параллельного и ортогонального к угловой скорости :

,   ,   ,  (17.8)

найдем, что

и скорость (17.7) принимает вид

                                                                               (17.9)

Рассмотрим орты естественных осей: касательной , главной нормали  и бинормали  окружности  в точке  (Рис.36). Векторы  и  могут быть записаны в виде ,  и скорость (17.9) получит окончательное представление

     .                                           (17.10)

Отсюда следует, что скорость направлена по касательной к окружности  (в сторону вращения), а модуль скорости равен произведению радиуса вращения точки  на угловую скорость вращения тела : .

Вектор скорости можно вычислять в подвижных и неподвижных осях.

В подвижных осях  компоненты, модуль и направление скорости (17.9) с учетом (17.5) соответственно равны

, , ,

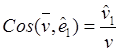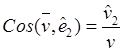,   ,   ,   ,                                (17.11)

а в неподвижных осях  соответствующие величины имеют значения

, , ,

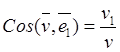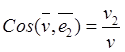,   ,   ,   ,                                (17.12)

где

,   .

Обратимся, далее, к вычислению ускорения произвольной точки тела при вращении. В соответствии с теоремой Ривальса ускорение точки  тела в произвольном движении равно сумме полюсного, вращательного и осестремительного ускорений:

.                                                                                                      (17.13)

Во вращательном движении ускорение полюса равно нулю: 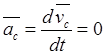, а угловая скорость и угловое ускорение параллельны друг другу и согласно (17.5), (17.6) соответственно равны

,   .

Следовательно, будут совпадать друг с другом радиусы-векторы  и  при вращении точки  вокруг осей, идущих в направлении  и :

.

Поэтому в (17.13) вращательное ускорение является касательным ускорением:

    ;

оно равно произведению радиуса вращения точки на угловое ускорение тела и направлено по касательной к окружности  (Рис.36), а осестремительное ускорение – нормальным ускорением

    ;

оно равно произведению радиуса вращения точки на квадрат угловой скорости тела и направлено по радиусу окружности  к ее центру (Рис.36).

Таким образом, во вращательном движении ускорение точки (17.13) равно векторной сумме касательного и нормального ускорений и, тем самым, лежит в плоскости окружности :

   .                                                                            (17.14)

Модуль ускорения пропорционален расстоянию точки до оси вращения

,                                                                                             (17.15)

а его направление образует с радиусом точки  угол , определяемый выражением