![]() Представим движение капли относительно земли (в системе
Представим движение капли относительно земли (в системе ![]() , связанной с землей) как сложное,
состоящее из относительного движения относительно пешехода (в системе
, связанной с землей) как сложное,
состоящее из относительного движения относительно пешехода (в системе ![]() , связанной с пешеходом) и переносного
движения самого пешехода
, связанной с пешеходом) и переносного
движения самого пешехода ![]() в системе
в системе ![]() . Тогда скорость капли
. Тогда скорость капли ![]() относительно земли является абсолютной,
скорость
относительно земли является абсолютной,
скорость ![]() пешехода – переносной
пешехода – переносной ![]() , а скорость капли
, а скорость капли ![]() относительно
пешехода – относительной. Зонт лучше всего защищает пешехода, когда скорость
относительно
пешехода – относительной. Зонт лучше всего защищает пешехода, когда скорость ![]() параллельна рукоятке зонта.
параллельна рукоятке зонта.
Теорема
сложения скоростей ![]()
![]() геометрически
выражается прямоугольным треугольником скоростей, в котором
геометрически
выражается прямоугольным треугольником скоростей, в котором ![]() является углом между гипотенузой
является углом между гипотенузой ![]() и катетом
и катетом ![]() (Рис.42).
Из этого треугольника следует выражение для искомого угла:
(Рис.42).
Из этого треугольника следует выражение для искомого угла: 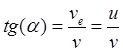 . Отсюда следует, что с ростом скорости
пешехода должен расти и угол
. Отсюда следует, что с ростом скорости
пешехода должен расти и угол ![]() , т.е. рукоятку зонтика
следует сильнее отклонять от вертикали.
, т.е. рукоятку зонтика
следует сильнее отклонять от вертикали.
7°. Зависимость между ускорениями точки в сложном движении.
При сложном
движении точки ![]() между ускорениями составляющих и
результирующего движений существует определенная зависимость, устанавливаемая
следующей теоремой сложения ускорений (теоремой Кориолиса).
между ускорениями составляющих и
результирующего движений существует определенная зависимость, устанавливаемая
следующей теоремой сложения ускорений (теоремой Кориолиса).
Теорема: Если точка совершает сложное движение, то в каждый момент времени ее абсолютное ускорение равно векторной сумме переносного, относительного и добавочного (Кориолисового) ускорений:
![]() ,
, ![]() .
(19.16)
.
(19.16)
Доказательство.
Возьмём абсолютную производную по времени от выражения для результирующей
скорости: ![]() , тогда будем иметь
, тогда будем иметь
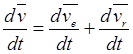 .
(19.17)
.
(19.17)
Здесь 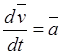 –
абсолютное ускорение точки. Вычислим выражения для каждого слагаемого в правой
части равенства (19.7). Первое слагаемое равно
–
абсолютное ускорение точки. Вычислим выражения для каждого слагаемого в правой
части равенства (19.7). Первое слагаемое равно
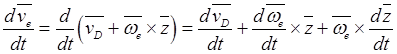 .
.
Так как
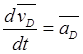 ,
, 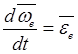 ,
, 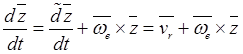 , то эта производная представима в
форме
, то эта производная представима в
форме
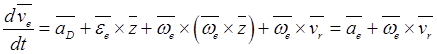 .
(19.18)
.
(19.18)
Здесь вектор ![]() характеризует изменение переносной
скорости
характеризует изменение переносной
скорости ![]() ,обусловленное движением среды
,обусловленное движением среды ![]() , а вектор
, а вектор ![]() – то
изменение
– то
изменение ![]() , которое обусловлено относительным
движением (поскольку разные точки среды имеют разные скорости).
, которое обусловлено относительным
движением (поскольку разные точки среды имеют разные скорости).
Рассмотрим, далее, второе слагаемое в правой части (19.17). Учитывая выражение относительного ускорения (19.3), имеем
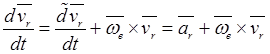 .
(19.19)
.
(19.19)
Первое слагаемое правой части ![]() представляет собою относительное
ускорение, оно учитывает изменение относительной скорости за счет
относительного движения. Второе слагаемое
представляет собою относительное
ускорение, оно учитывает изменение относительной скорости за счет
относительного движения. Второе слагаемое ![]() определяет
то изменение
определяет
то изменение ![]() , которое обусловлено переносным движением
(вращением среды). Подстановка выражений производных
, которое обусловлено переносным движением
(вращением среды). Подстановка выражений производных 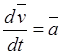 и
(19.18), (19.19) в равенство (19.17) приводит к представлению абсолютного
ускорения точки
и
(19.18), (19.19) в равенство (19.17) приводит к представлению абсолютного
ускорения точки
![]() , которое и доказывает теорему.
, которое и доказывает теорему.
Итак, в
сложном движении точки правило сложения ускорений сложнее, чем для скоростей:
для получения абсолютного ускорения к сумме относительного и переносного ускорений
требуется добавить еще вектор добавочного (Кориолисового) ускорения. Выше
объяснено, что возникновение этого ускорения связано с изменением ![]() за счет относительного движения и с
изменением
за счет относительного движения и с
изменением ![]() за счет переносного движения.
Замечательным является то обстоятельство, что влияние обоих этих факторов
одинаково. Формула (19.16) геометрически означает, что абсолютное ускорение
является замыкающей ломанной линии, звеньями которой служат переносное,
относительное и добавочное ускорения (Рис.43).
за счет переносного движения.
Замечательным является то обстоятельство, что влияние обоих этих факторов
одинаково. Формула (19.16) геометрически означает, что абсолютное ускорение
является замыкающей ломанной линии, звеньями которой служат переносное,
относительное и добавочное ускорения (Рис.43).
![]() Чтобы аналитически определить абсолютное ускорение, найдем,
например, его компоненты в подвижных осях
Чтобы аналитически определить абсолютное ускорение, найдем,
например, его компоненты в подвижных осях ![]() ,
считая заданными относительное и переносное движения точки. Согласно (19.16)
,
считая заданными относительное и переносное движения точки. Согласно (19.16)
![]() ,
,
![]() ,
, 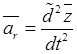 ,
, ![]() , поэтому компоненты абсолютного
ускорения в подвижных осях будут равны
, поэтому компоненты абсолютного
ускорения в подвижных осях будут равны
![]() ,
, ![]() ,
(19.20)
,
(19.20)
где
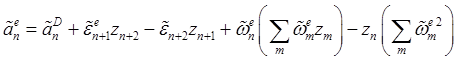 ,
,
![]() ,
, ![]() ,
, ![]() .
.
По компонентам (19.20) величина и ориентация абсолютного ускорения в подвижной системе координат определяются формулами
![]() ,
, 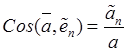 ,
, ![]() .
(19.21)
.
(19.21)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.